Sistemul forței-forță-forță spațială nu se află într-un singur plan și liniile lor de acțiune nu se intersectează într-un singur punct.
Pentru a considera un astfel de sistem de forțe, este necesar să introducem noi concepte:
1. Moment de forță față de centru în spațiu.
2. Momentul de forță în raport cu axa.
3. Momentul unei perechi de forțe în spațiu.
Momentul de forță în jurul centrului în spațiu - o cantitate vectorială, care este egală cu produsul vectorial al vectorului razei trase dinspre centru spre punctul de aplicare a forței, și vectorul forței.
Prin definiție, cruce momentul vector produs de forță este direcționată perpendicular trasată prin planul central și putere în direcția de rotație a vectorului razei la forța vectorului vizibil invers acelor de ceasornic, la cel mai mic unghi.
Modulul vectorului de moment unghiular față de centru este egal cu:
. Modulul vectorului de moment unghiular față de centru este numeric egal cu dublul ariei triunghiului.
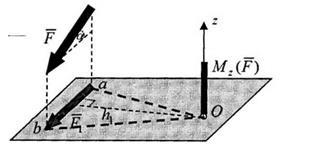
Momentul forței în raport cu axa este egal cu două ori aria triunghiului.
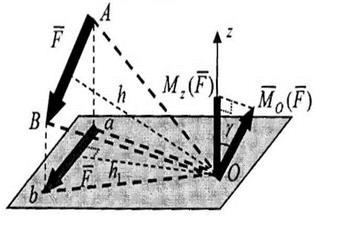
Relația momentului de forță cu centrul și cu axa.
Modulul vectorului de moment unghiular față de centrul care se află pe axa z este egal cu dublul suprafeței triunghiului OAB:
Momentul forței în raport cu axa z este de două ori aria triunghiului. . Triunghiul triunghi OAB obținut prin proiecție pe un plan perpendicular pe axa z, iar suprafața sa este legată de aria triunghiului OAB relație. unde este unghiul dihedral dintre planurile triunghiurilor. Deoarece forța vector momentul în jurul unui punct perpendicular pe planul triunghiului OAB, unghiul dintre vectorul și axa egal cu unghiul. Astfel, momentul de forță raportat la axă este proiecția vectorului momentului unghiular față de centrul pe această axă:
Momentul de cuplu forță în spațiu - vector perpendicular pe planul de acțiune al perechii îndreptate spre direcția din planul de rotație sub influența perechii pare să se întâmplă invers acelor de ceasornic. Modulul vectorului de moment al perechii este egal cu produsul uneia dintre forțele perechii de pe brațul perechelui:
Teoreme pe perechi. (teoremele sunt date fără dovadă)
La transferul unei perechi de forțe într-un plan paralel cu planul acțiunii sale - O pereche de forțe poate fi transferată în orice plan paralel cu planul acțiunii sale. Starea cinematică a corpului nu se schimbă.
Cu privire la echivalența perechilor de forțe - O pereche de forțe poate fi înlocuită de o altă pereche de forțe, dacă momentele lor sunt geometric (vectoriale) egale. Starea cinematică a corpului nu se schimbă.
La adăugarea de abur forțează avionul - cupluri de forță sistem pe planul poate fi înlocuit cu o pereche, care este punctul geometric (vector) suma momentelor de perechi inițiale. Starea cinematică a corpului nu se schimbă. Condiția de echilibru pentru sistemul de perechi de forțe -
Apoi, vom continua să aderăm la planul general de studiu al sistemului de forțe, abordând în mod consecvent trei aspecte:
1. Cum să simplificați sistemul?
2. Care este cel mai simplu tip de sistem?
3. Care sunt condițiile pentru echilibrul sistemului?
Aducerea unui sistem arbitrar de forțe la un centru dat - alegeți un punct arbitrar pe plan și pe fiecare dintre forțe
transferăm prin metoda Poinsot la acest punct.
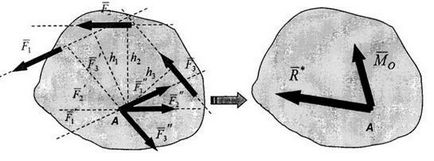
În locul sistemului original arbitrar, obținem un sistem convergent de forțe și un sistem de perechi.
Spre deosebire de sistemul arbitrar de forțe, considerat anterior, care utilizează acum metoda Poinsot, perechile de forțe atașate sunt caracterizate de vectori.
Sistemul forței convergente este redus la o forță aplicată în centrul turnului ().
Sistemul de perechi este redus la o pereche, momentul fiind egal cu suma vectorilor momentelor forțelor inițiale față de centrul reducerii ().
În general, un sistem plan arbitrar de forțe este redusă la o forță, numită vectorul principal și perechea de un cuplu egal cu punctul principal al sistemului de forțe pentru adaptarea centrului:
. unde este vectorul principal; este momentul principal.