Ridicați exponentul în gradul de matrice, adică găsiți unde. Cazul valorilor proprii complexe.
Plan: Vom găsi soluții particulare ale sistemului în condițiile inițiale. iar exponentul matricei cerut va fi o matrice, unde aceste soluții particulare vor fi scrise în coloane.
soluţie:
În primul rând, găsim valorile proprii ale acestei matrice:
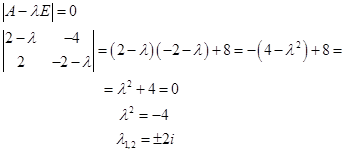
Acum găsim vectorii proprii:
1)
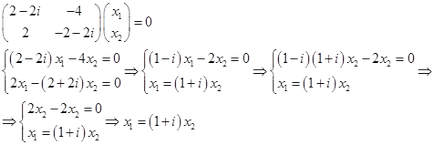
În acest caz, pentru un eigenvector, luăm:
Cel de-al doilea eigenvector pentru noi în acest caz fără nevoie, totul este tot conjugat. Să continuăm.
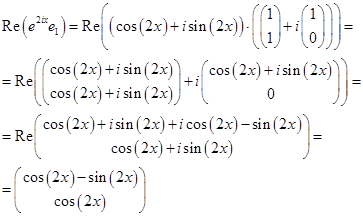
Apoi, printr-o soluție generală a sistemului de ecuații diferențiale
va:
Și găsim o soluție specială în condițiile inițiale: și.
1). înlocuim în soluția generală:
Și decizia privată va lua forma:
2). înlocuim în soluția generală:
Și decizia privată va lua forma:
Să scriem aceste soluții în coloane:
O verificare poate fi făcută folosind pachetul matematic Maple, adică calculați exponentul matricei în Maple.
Mai întâi trebuie să conectați biblioteca de funcții pentru algebra liniară:
> cu (linalg);
Și apoi urmează să scrieți acest lucru:
> exponențială (, x);
Maple vă va oferi acest lucru:

Asta coincide cu răspunsul nostru.