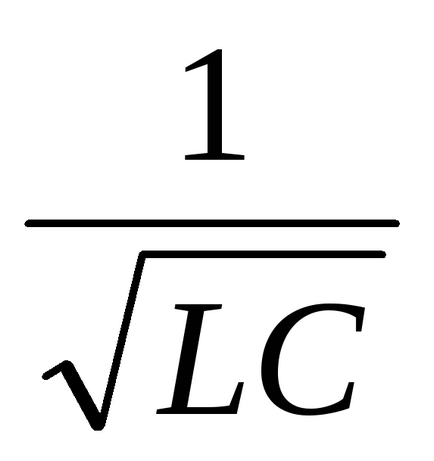Scopul lucrării este de a studia particularitățile proceselor tranzitorii în circuitele electrice care conțin dispozitive de stocare a energiei, pentru a obține o idee despre condițiile de existență a regimurilor staționare în circuit și legătura acestora cu regimul forțat.
1. Tezele de bază ale teoriei
Lanțuri care conțin numai elemente rezistive nu se acumulează energie electrică pentru comunicarea între reacția și impactul descrie un factor constant care este independentă de starea anterioară a circuitului și este determinată de schema de conexiuni și parametrii elementelor rezistive.
Catenele electric diferit se poart conțin acumulatori reactive de energie electrică (inductanță, capacitate). În acest caz, energia generată de surse, sau transformat ireversibil în alt tip de energie consumată sau când se lucrează sau se acumulează în lanțul de unități cu jet. În această reacție în lanț la influență externă depinde nu numai de natura impactului, dar și asupra rezervelor de energie ale unităților cu jet.
Procesele asociate cu schimbarea energiei pe inelele de stocare se numesc procese tranzitorii.
Aproape toate circuitele care conțin elemente reactive se află într-o stare de tranziție tot timpul. Cu toate acestea, există regimuri în circuitele electrice, pentru care, practic, nu se modifică rezervele de energie în elementele reactive, sau schimba unele din legea periodice (în acest caz, nu se schimba valoarea medie a energiei pentru perioada stocată în elementele reactive). Aceste moduri sunt numite cvasi-constantă sau starea de echilibru au loc în lanțuri care conțin surse cu constantă sau periodică în parametrii de timp.
Procesele tranzitorii în circuitele electrice liniare sunt descrise prin ecuații diferențiale liniare. Soluția completă a acestor ecuații este de obicei considerată ca fiind suma soluțiilor generale și particulare. Soluția particulară nu depinde de rezervele de energie ale elementelor reactive și este determinată de surse externe, precum și de configurația și parametrii elementelor de circuit. A fost numită componentă forțată. Soluția generală este determinată în principal de starea dispozitivelor de stocare reactivă, rezervele lor de energie, forma sa nu depinde de surse externe, se numește componentă liberă.
Forma soluției pentru componenta liberă depinde de rădăcinile ecuației caracteristice și poate fi reprezentată în formă
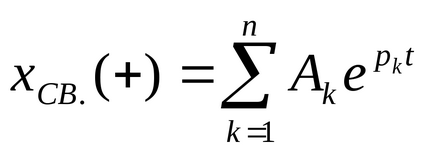
În lanțurile liniare, existența rădăcinilor cu o parte reală nu este posibilă decât în lanțurile fără pierderi care constau numai din elemente reactive. În acest caz, în lanț apar oscilații nesimetrice. Întrucât, în practică, astfel de lanțuri nu există, cercetarea lor este pur teoretică.
De interes special sunt lanțurile cu elemente ireversibile active (amplificatoare operaționale etc.), care din punct de vedere teoretic pot fi considerate ca lanțuri care conțin elemente cu parametri negativi. În acest caz, ecuația caracteristică are rădăcini cu o parte reală pozitivă, în timp ce componenta liberă poate crește fără limită.
În circuite reale, acest mod este imposibil, deoarece într-o anumită etapă circuitul intră într-un mod neliniar, la care se oprește creșterea suplimentară a componentei libere.
În această lucrare de laborator, aceste regimuri nu sunt luate în considerare. Deoarece circuitele pasive cu pierderi componentă liberă este întotdeauna amortizată prin estimarea atenuare durata procesului de tranziție, care introduce conceptul de degradare τ constantă. τ - intervalul de timp, în care componenta liberă după scade cu un factor e (e = 2,71828 ...).
Durata procesului tranzitoriu este de obicei considerată egală cu (3 ÷ 4) τ. După această perioadă de timp, valoarea reziduală a componentei libere este egală cu o sută din valoarea sa inițială.
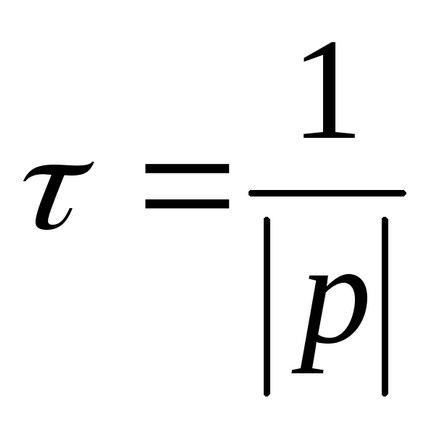
p1,2 = - δ ± јω. Constanta de timp este determinata de formula
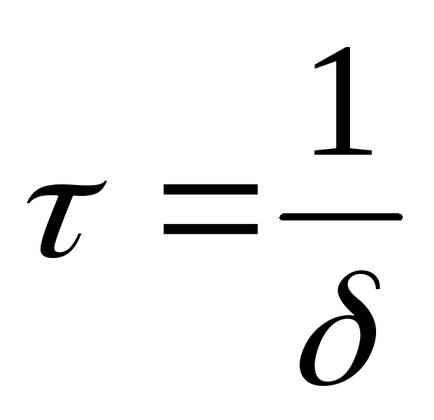
Să analizăm caracteristicile proceselor tranzitorii în circuitele de ordinul I și II. Cele mai evidente procese tranzitorii pot fi studiate la conectarea circuitului la o sursă constantă. Întrucât în acest caz componenta forțată are o valoare constantă, componenta liberă poate fi izolată în formă pură și observată pe ecranul osciloscopului.
Într-o instalație de laborator, un generator de impulsuri de formă dreptunghiulară este de obicei utilizat pentru studierea tranzitorilor, în timp ce durata impulsului (pauză) este aleasă astfel încât să fie comparabilă cu constanta de timp a procesului tranzitoriu.
Perioada de repetare a impulsului este T = 1 / f. unde f este frecvența oscilatorului principal. Deoarece durata impulsurilor este egală cu durata întreruperilor dintre ele, tu = 1 / 2f.
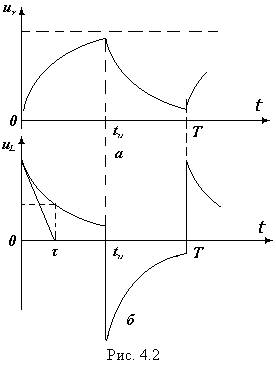
Circuitul echivalent calculat, de exemplu, circuitul r-L, în intervalul impulsului prezentat în Figura 4.1 și corespunde includerii tsepir constantă sursă Lc-emf, iar intervalul de pauză - prin ris.4.1.b (scurt-circuit tsepir-L). Oscilogramele tipice ale acestui experiment sunt prezentate în Fig.4.2.
Deoarece în regiunea de rezistență r tensiunea și curentul sunt conectate printr-un tur relativ direct proporțional = i · r. curba de tensiune (t) la scara corespunzătoare este de asemenea curba curentă în circuitul i (t).
Din oscilograma nu este dificil să se determine constanta de timp τ. Este egal cu un segment din taiga, construit în conformitate cu figura 4.2 (B). Pentru circuitul r-L, constanta de timp este L / r. pentru lanțul C, valoarea lui -C. Mai exact, este posibil să se determine din oscilograma constanta de timp bazată pe faptul că. după cum am menționat deja. pentru un timp τ, componenta liberă scade cu un factor de 2,72 și este de aproximativ 0,37 din valoarea sa maximă (figura 4.2b). În ambele cazuri, este mai întâi necesar să se determine intervalul de timp pentru o anumită oscilogramă (valoarea lui T = 1 / f este cunoscută).
Procesele tranzitorii în lanțuri cu două elemente reactive au un caracter mai complex. În acest caz, în funcție de rădăcinile ecuației caracteristice, ele sunt fie aperiodice, fie oscilante. De exemplu, în cazul unei conexiuni seriale a elementelor, dacă relația r> 2
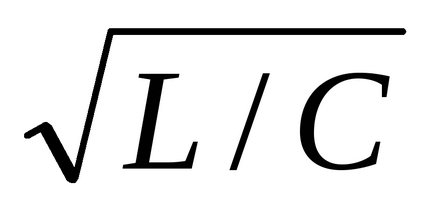
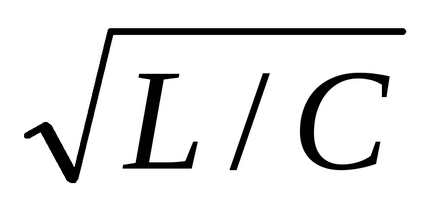
r = 2
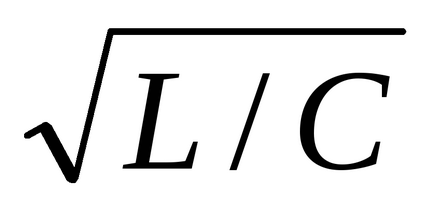
În procesul oscilator, cantitatea r / 2L caracterizează rapiditatea decăderii procesului, cu constanta de amortizare = 2L / r. Frecvența oscilațiilor care apar în acest caz este determinată din relație
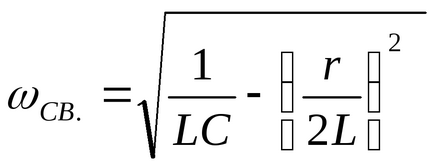
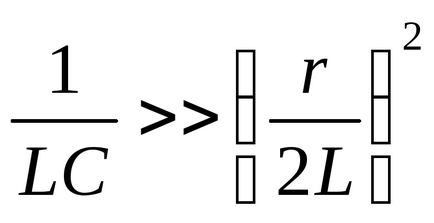
ωSV. ≈ω0 =