4. Găsiți cea mai mare soluție intregă a inegalității:
Noi multiplicăm ambele părți ale inegalității cu 15 - cel mai mic numitor comun al acestor fracțiuni. Obținem inegalitatea echivalentă:
3 · (x-2) -5 · (2x + 3)> 15. Extindeți parantezele: 3x-6-10x-15> 15 și simplificați:
3x-10x> 15 + 6 + 15. Obținem -7x> 36. Împărțim ambele părți ale inegalității printr-un coeficient negativ pentru x, deci schimbăm semnul inegalității în contrariul:
x<-36/7. Выделим целую часть и покажем решения неравенства на числовой прямой.
Cel mai mare număr întreg din intervalul umbrit este numărul -6.
5. Stabiliți soluția corectă a inegalității: log2 (x-4) ≤3.
Reprezentăm numărul 3 sub forma unui logaritm cu baza 2.
log2 (x-4) ≤ log2 2 3; deci log2 (x-4) ≤log2 8. Deoarece funcția logaritmică a bazei 2 este în creștere la mulțimea tuturor numerelor întregi pozitive, acestea din urmă inegalitatea ar fi realizată cu condiția ca x-4≤8, dar în același timp: x-4 > 0. Prima condiție presupune: h≤12, iar al doilea ca x> 4. Valoarea lui x∈ (4; 12) este comună.
7. Specificați funcția al cărei grafic este prezentat în figură.
În figură, vedem o parabolă care poate fi dată printr-o ecuație de formă: y = a (x-m) 2 + n, unde (m; n) sunt coordonatele vârfului parabolei. În figură, vârful parabolei este punctul (2; 1). Prin urmare, m = 2; n = 1. Și cum rămâne valoarea coeficientului a. Ne uităm la răspunsurile: pretutindeni, coeficientul anterior brațului este egal cu unul. Ei bine, grijile mai mici! Am obținut formula: y = (x-2) 2 + 1.
11. Lungimea secțiunii rectangulare este de 120 m, iar lățimea este de 75% din lungime. A aratat 35% din acest teren, apoi nu a arat:
Prin convenție, lățimea este de 75% de 120 de metri - lungimea sitului. Aceasta este de 3/4 din lungime, adică 120: 4 · 3 = 90 de metri. Suprafața porțiunii dreptunghiulare de lungime egală cu porțiunea de produs în lățimea sa, înseamnă 120 m · 90m = 10800 m 2 plug 35%, prin urmare, nu arat 100% -35% = 65%. Rămâne de a găsi 65% din 10800. procente în fracție zecimală Vă rugăm: 65% = 0,65, și se înmulțește această fracțiune de 10800.
0,65; 10800 = 7020. Răspundem la întrebarea problemei: 7020 m 2 nu este arat.
12. Rezolvați ecuația:
În partea dreaptă a ecuației aplicăm identitatea logaritmică de bază:
Prin urmare, am obținut puteri egale pe baza a 2, iar exponenții acestor grade vor fi egali. Rezultatul este o ecuație patratică: x 2 + x = 2 sau x 2 + x-2 = 0. Prin teorema lui Viet, alegem rădăcinile: x1 = -2; x2 = 1.
14. Rezolvați ecuația: sin 2 x-cos 2 x = cos (x / 2).
Prin formula cosinusă a unghiului dublu: cos2α = cos 2 α-sin 2 α, atunci această ecuație este transformată în forma:
-cos2x = cos (x / 2) ⇒ -cos2x-cos (x / 2) = 0 ⇒ cos2x + cos (x / 2) = 0. Suma cosinelor se transformă într-un produs folosind formula:
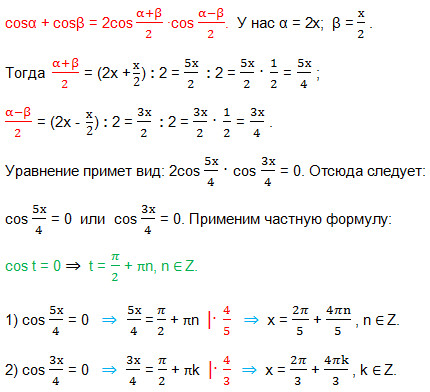
17. Găsiți suma ordonatelor punctelor extreme ale funcției f (x) = x 3 / (x 2 -3).
Desigur, știți că extremele sunt minime și maxime ale unei funcții care sunt posibile numai în punctele critice. Soluția clasică a acestei probleme: 1) găsiți derivatul unei funcții date; 2) găsiți punctele critice și marcați-le pe linia numerică; 3) determină semnele derivatului la intervale definite de punctele critice; 4) aflați care dintre punctele critice sunt punctele minime și care sunt punctele maximului; 5) găsiți valorile funcției însăși la aceste puncte minime și maxime - acestea sunt coordonatele punctelor extreme; 6) adăugați aceste valori de ordonare. Dar în această sarcină specială, totul este mult mai ușor! Funcția ne este dată ciudată, adică pentru toate valorile posibile ale lui x se menține următoarea egalitate: f (-x) = f (x). Graficul funcției ciudate este simetric cu privire la origine. Ce înseamnă acest lucru și cum ne ajută acest lucru? Susținem: dacă această funcție are un maxim într-un punct cu abscisa a. atunci la un punct simetric cu abscisa (-a), va avea un minim. Din nou, valorile funcției în aceste puncte a și -a vor fi, de asemenea, numere opuse. Și care este suma numerelor opuse? Corect: zero. Concluzie: dacă trebuie să găsiți suma ordinelor punctelor extremum cu o funcție ciudată, atunci răspunsul este: 0.
21. Găsiți suma rădăcinilor ecuației: x -2 -16x -1 -80 = 0.
Să facem o substituție: x -1 = y. Obținem ecuația: y 2 -16y-80 = 0. Găsiți rădăcinile: y1 = -4 și y2 = 20.
Apoi x -1 = -4 sau x -1 = 20.
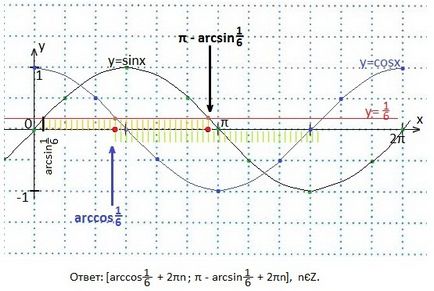
22. Rezolvați sistemul de inegalități:
Într-un sistem de coordonate, reprezentăm funcțiile y = sinx, y = cosx și y = 1/6. Definim intervalul de valori al lui x pentru care curba sinusoidală este mai înaltă, iar graficul cosinus este sub linia dreaptă y = 1/6.
24. Găsiți zona paralelogramului ABCD dacă A (5; 4); B (0; 3); C (4; 7); D (9; 8).
Zona paralelogramului se găsește prin formula: S = absinA, unde a = AD și b = AB - laturile paralelogramului, iar A este unghiul dintre aceste laturi. Folosim vectori: găsim coordonatele și modulele vectorilor care exprimă laturile AD și AB ale paralelogramului, cosinusul unghiului dintre aceste vectori. Apoi găsim sinusul acestui unghi, iar în formula zonei paralelogramului înlocuim toate valorile necesare.

25. Ceasul electronic arată ora în ore și minute (de la 00:00 la 23:59). De câte ori pe zi puteți vedea pe tabloul de bord 4 cifre 2, 0, 1, 9 (în orice ordine). Deoarece nu, de exemplu, 91 de minute sau 29 de ore, combinatorii nu ne vor ajuta. Pur și simplu vom enumera toate posibilitățile citirilor în timp real.
Prieteni, repetați formula. Vă urez succes!