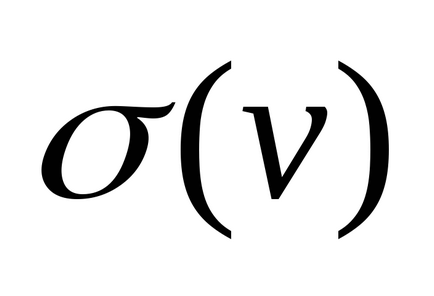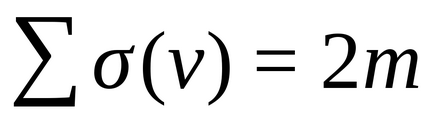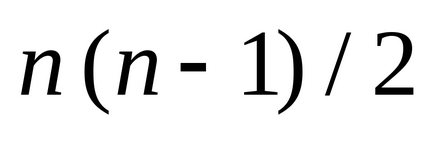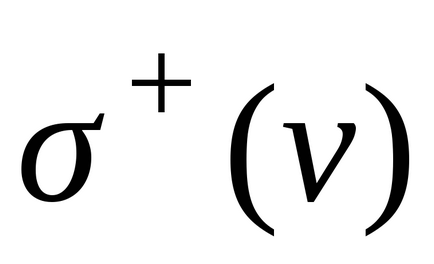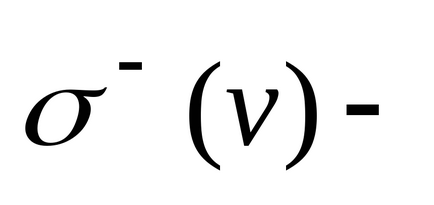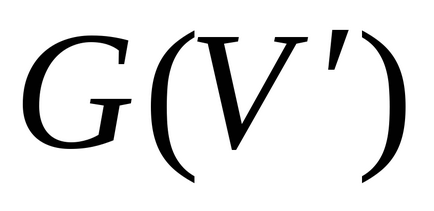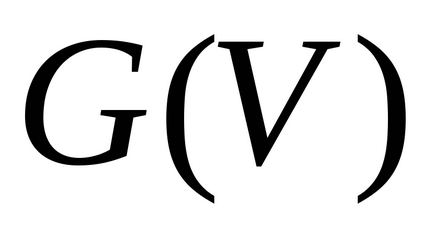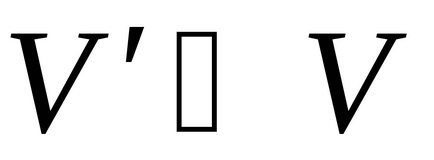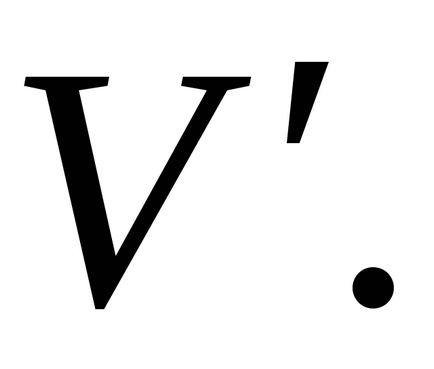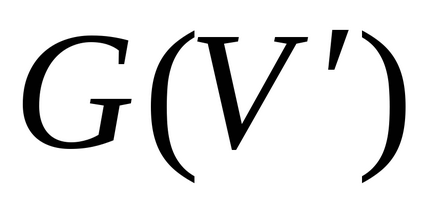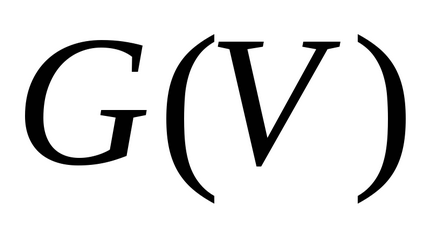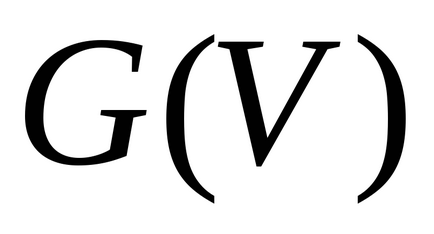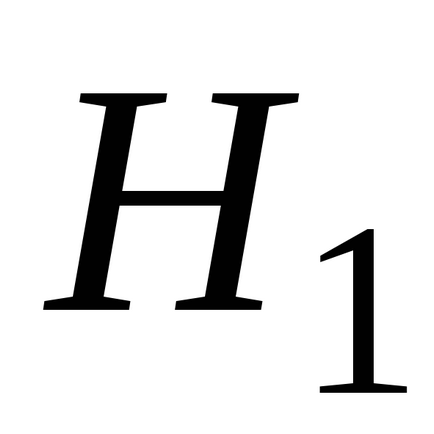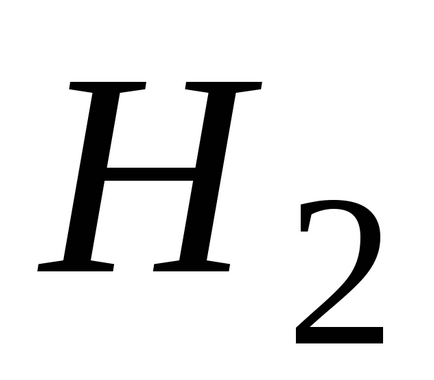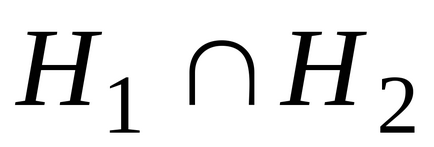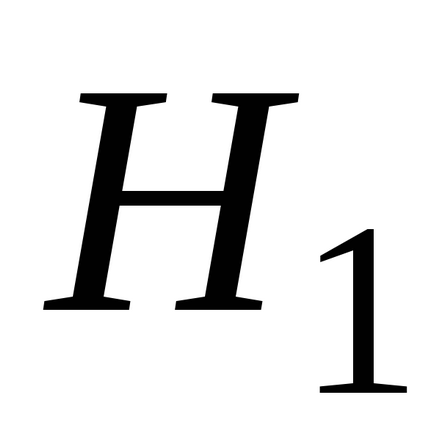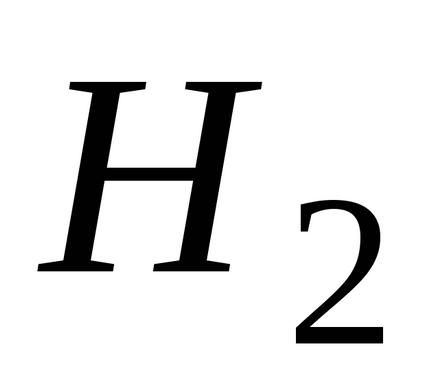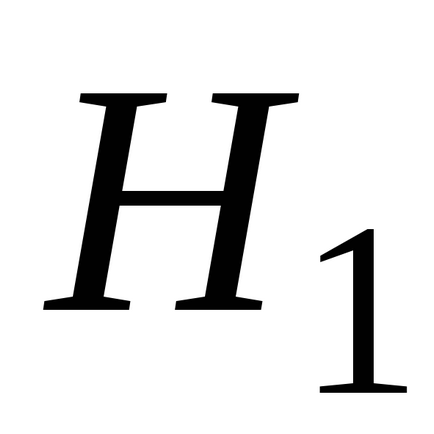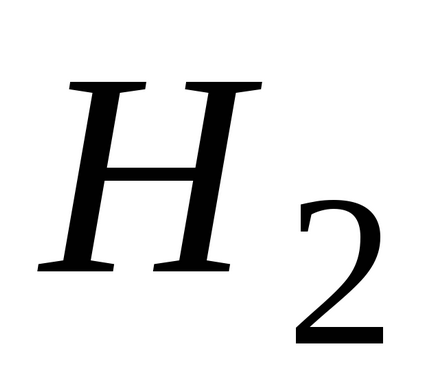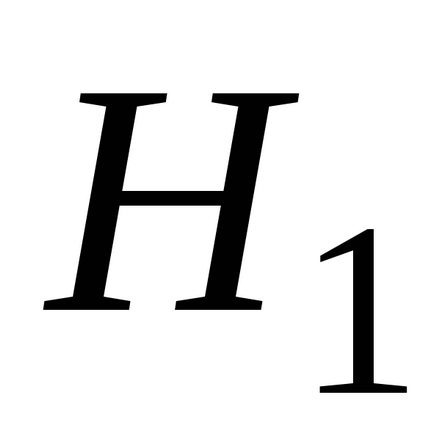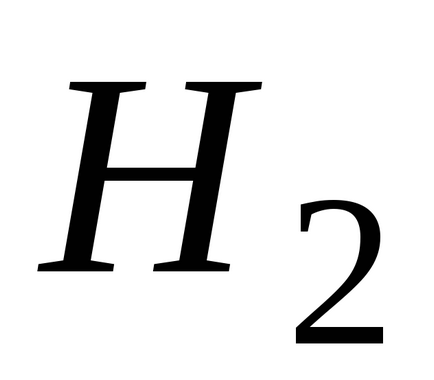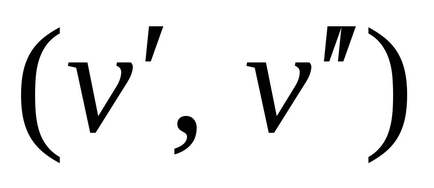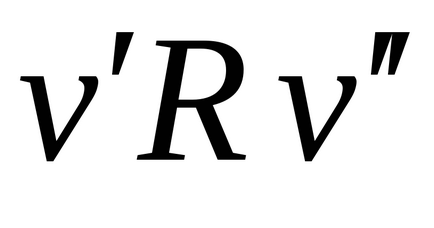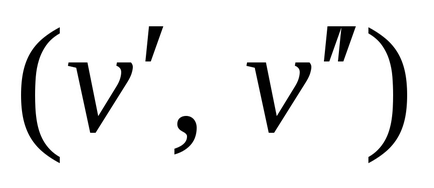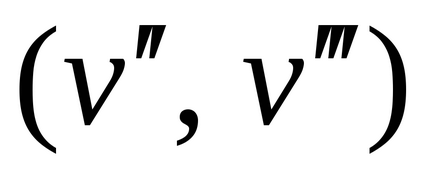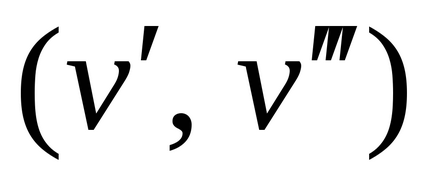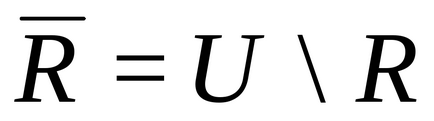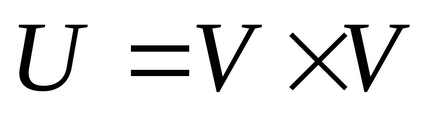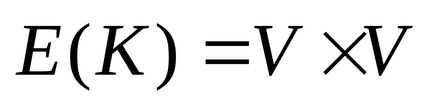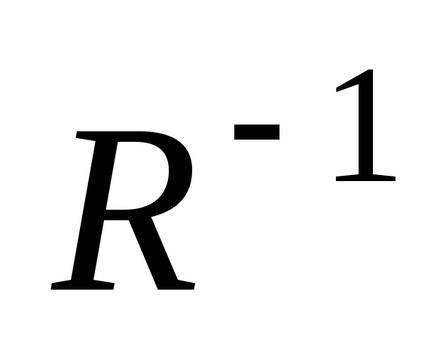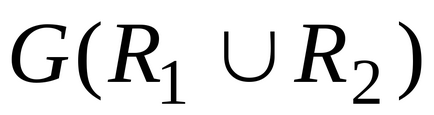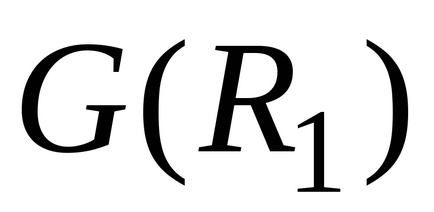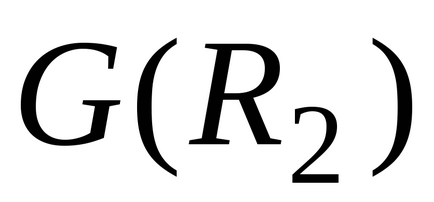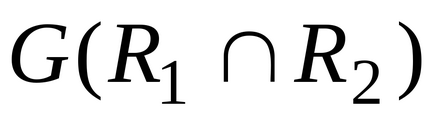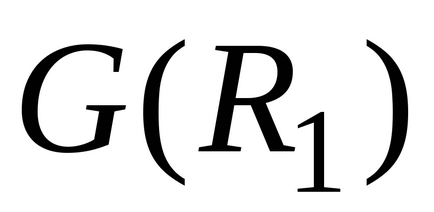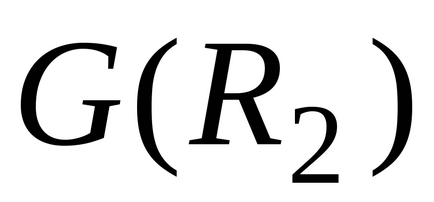(Local) sau (valență)
nodurile reprezintă numărul de margini care intră în contact cu vârful v.
Dacă nu se specifică altfel, bucla este calculată de două ori la calcularea valenței vârfului.
Un grafic este corect (cu valența r) sau grafic r-valent (regulată, uniformă), în cazul în care toate nodurile grad egal.
Vârful este numit izolat. dacă nu este învecinată cu niciunul dintre vârfurile graficului, sau, care este același, ne-incidental la orice margine. Gradul acestui vârf este 0.
Un vârf având un grad egal cu 1 este numit un punct de suspendare (terminal). O margine, un vârf incidental, se numește margine terminală.
Declarația 1. (handshakes lemma): În n-graf, suma gradelor tuturor vârfurilor este egală cu dublul numărului de margini (adică, chiar):
. unde m este numărul de margini.
Corolar 1. Un grafic arbitrar are un număr par de vârfuri de grad impare.
Corolar 1. Numărul de margini din graficul complet este
. unde n este numărul de vârfuri.
În ortograma există două grade (locale) ale vârfului:
și numărul de margini cu un început și un sfârșit în v, respectiv.
Aserțiunea 2. Sumele de grade ale tuturor vârfurilor unei ortograme sunt egale cu numărul marginilor acestui grafic și, prin urmare, sunt egale una cu cealaltă :. m este numărul de margini.
Piese, subgrafe și subgrafe
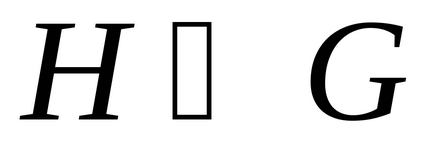
Un grafic H este numit o parte a graficului G (
) dacă mulțimile vârfurilor și muchiilor sale sunt cuprinse în seturile de vârfuri și marginile graficului G.
Dacă setul de noduri ale grafului H și graficul G coincid, apoi grafH numit parțial graph G. graph parțial H se numește un capac pentru n-graf G. Dacă fiecare vârf al graficului G intsindentna cel puțin o margine a NA (de exemplu, în cazul în care G nu are noduri izolate, atunci supara nu trebuie să aibă noduri izolate).
subgrafic
coloanăcu multe noduriSe numește partea graficului la care toate marginile sunt incidentale
(Subgraful
pot fi obținute din graficprin ștergerea unora dintre nodurile și / sau marginile graficului. În acest caz, dacă ștergem vârful, atunci ștergem neapărat toate marginile care îi sunt incidentale).
Operații asupra unor părți ale graficului
plus
la partea H este determinată de mulțimea tuturor muchiilor lui G. Nu aparține lui H:
, ;
sumă
Piese și grafic G. este graficul al cărui
Lucrarea
Piese și grafic G. este graficul al cărui
Piese
și Nu intersectează nodurile dacă nu au noduri comune și, prin urmare, muchii comune:
, .
Piese
și Nu se intersectează de-a lungul marginilor dacă
.
Dacă, atunci suma
numită linie dreaptă.
Grafice și relații binare
Un grafic orientat G (R) cu mai multe vârfuri V cu un set de vârfuri V în care marginea
există numai dacă este îndeplinită. OtnosheniyuR reciproc simetrice corespunde în mod unic graf neorientat fără margini paralele G (R) R .Antisimmetrichnomu relație bijectivă corespunde graficului direcționat, fără margini paralele care nu conțin perechi de noduri cu nervuri, oppositely direcționate spre înălțimi diferite. Dacă este reflexiv. atunci graficul G (R) fără muchii multiple are bucle la toate vârfurile. Dacă Rantirefleksivno, atunci graful G (R), fără margini multiple nu are bucle. Dacă este tranzitorie. apoi în graficul G (R) fără muchii multiple pentru fiecare pereche de muchii șiexistă o margine posterioară. lăsa- adăugarea raportului R la V. , unde U este raportul universal (total) , și anume relația care are loc între orice pereche de elemente din V.
Graficul G (
) este complementul graficului G (R) (până la un digraph complet K cu setul de vârfuri V și setul de muchii ).
Graficul relației inverse G (
) diferă de graficul G (R) în sensul că direcțiile tuturor muchiilor sunt inversate.
Graficul grafic al unirii a două relații definite pe V,
este un grafic al sumei a două graficeși:
.
Graficul grafic al intersecției relațiilor pe V,
este graficul de intersecție al două graficeși:
.