proiecție cilindrică Conformal
Mercator
Proiecția cilindrică Conformal a fost propusă pentru prima dată și folosit în 1569 de cartograful olandez Mercator.
Pentru a obține formulele din această proiecție este definită prin paralele prima scala în cea mai simplă dintre proiecțiile cilindrice din așa-numita proiecție pătrat. Meridianele și paralelele sunt desenate prin același număr de grade de longitudine și latitudine pe pătrate formă hartă grilă, lungimea stocată în toate meridianele și ecuatorul (proiecție echidistante).
Să PC0A0 și PD0B0 (Fig. 1) de pe glob -meridiany raza R cu diferenta infima de longitudinile și directă
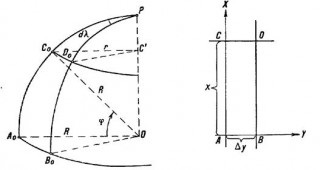
Fig. 1. Două meridiane și două paralele de pe glob și pe hartă într-o proiecție cilindrică
CA și DB - meridiane legate de pe hartă în proiecția pătrat.
Apoi, un segment infinitezimal S0D0 orice paralele cu latitudinea și raza r de pe glob se vor întâlni pentru a cartografia segmentul CD infinitezimal, iar scara de paralela
.
În cazul în care A0B0 - un arc de ecuator.
Deoarece raportul dintre arce egal cu raportul razelor acestora,
De la OS 0C“. Sistem de operare în cazul în care 0C = Avem
,
Formula arată că scara proiecțiilor paralele din piață se schimbă de la una la infinit, și este egal cu unitatea la ecuator (pentru j = 0 °), iar infinitatea în poli punct (la = 90 °). Polul în proiecția pătrat este reprezentată printr-un segment de linie egală cu lungimea ecuatorului.
Acum, pentru a face scara meridiane scară egală de-a lungul paralelelor (m = n), t. E. Pentru a trece de proiecție pătrat la CONFORMAL (distorsiuni elipse cercurilor) Must meridianele de proiecție pătrat de întindere la fiecare punct de câte ori vor fi timp paralel cu această proiecție a crescut în raport cu paralelele corespunzătoare ale globului, t. e. dintr-o dată. Prin urmare, pentru convertirea o primă aproximare, un reticul pătrat GRATICULES proiecție conformal trebuie meridianul segmente OA, AB, BC, și așa mai departe. D. (Fig. 2), respectiv, se multiplică
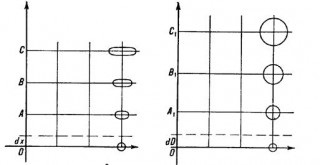
Fig. 2. Transformarea proiecțiilor pătrate în conformal cilindrice
1, 2, 3, etc., unde 1,2, 3, - .., respectiv latitudinea acestor segmente ale punctelor mediane. Apoi segment meridianul de proiecție conformal OC1 care corespunde segmentului care operează într-o proiecție pătratică, dată de expresia
Și segmentele
Meridian segmentul OS 1 va fi definit mai precis, mai mici vor fi luate segmentele sale constitutive, meridiane de întindere trebuie să fie continuu de la ecuator la această paralelă.
Cele mai precise rezultate sunt obținute atunci când secțiunea meridianul D în proiecția Mercator va consta din suma unui număr infinit de mare de cantități infinit de mici
,
În cazul în care Dx - un segment infinitezimal al unui meridian în pătratul proiecției,
DD - corespunzător segmentului infinitezimal al unui meridian în proiecția Mercator CONFORMAL. Dar, având în vedere constanța meridianele într-un interval de scală de proiecție pătrat
,
Suma cantităților infinit de mici în matematici superioare se numește integrală. Ia integralei ambelor părți înseamnă să ia suma cantităților infinit de mici ale acelor părți ale egalității într-un anumit interval.
Integrala de exprimare în sensul latitudinea de la 0 pentru a scrie ca
Ca urmare a integrării în partea stângă a ecuației obținem o secțiune meridianul de D; pe partea dreaptă a tabelului reprezintă egal integrantă
Astfel, lungimea unui meridian
.
unde C este o constantă de integrare.
Valoarea C trebuie să fie constantă pentru toate valorile latitudine, astfel încât este ușor să se determine, luând = 0 °. Când = 0 ° corespunde ecuator paralel, pentru care D = 0, adică. E.
,
Trecând de la logaritmul natural în zecimal și exprimarea cardului D și scala principală în centimetri va avea o formulă finală de lucru pentru calcularea meridian intervalului equiangular D într-o proiecție cilindrică a unei sfere
Formula arată că secțiunea meridianul de pol la D (= 90 °) este egal cu infinit, r. E. Terminal pe o hartă în această proiecție nu este afișată.
Luând Pământul pentru un elipsoid, avem formula
În cazul în care o - raza de ecuatorul elipsoidului pământului (exprimată în metri)
U - aceeași cantitate ca în formula (22) Conformal CONIC.
Distanțele între meridianele din proiecțiile equiangular ca într-un proiecții pătrat definit prin formula
,
În cazul în care și-a exprimat în radiani. Luând Pământul pentru un elipsoid, și care exprimă scara principală hartă în țoli, avem
Adesea, această formulă este scris ca
În cazul în care Y - distanța de pe hartă meridianul centrală pentru a determina
° este diferența în meridiane medii și longitudini definite, exprimate în grade, ° = 57 °, 3.
Este evident că deformarea în proiecție cilindrică conformal pe cilindrul tangent vor fi exprimate prin formulele
Pentru a calcula meridianul segmente D, iar în scara ordonată în proiecție cilindrică conformal pe cilindrul secantă formulele de lucru vor avea forma
Acolo unde raza r0- a secțiunii paralele cu o lățime de 0 pe elipsoid pământ,
r-rază paralelă cu latitudinea pe elipsoid pământ, care este determinată de scara,
este o scara principală a hărții,
° - diferența de longitudine și meridiane secundare determinate, exprimate în grade.
Reticul în Mercator
Pentru a construi reticul în Mercator și aplicarea punctelor de referință pentru cartografierea trebuie să cunoască coordonatele rectangulare (segment D meridian și ordonata y) ale punctelor de intersecție dintre meridianele și paralelele și baze.
Valoarea argumentului medie latitudinea D selectate din tabele speciale compilate hidrografice Marinei operate, iar valoarea y se calculează conform formulei (35).
Ca origine pe topuri este luată în punctul de intersecție al meridianului de mijloc și de bazin maritim principal în paralel, pentru care cartografiere. Această paralelă este secțiunea paralelă, și este egală cu o scală.
Cunoscând coordonatele rectangulare ale vârfurilor unghiurilor dincolo de foaia de card, sunt dimensiuni ale laturilor cadru ca și diferența de secțiuni meridianul D la sud și la nord latitudine și diferența de valori y pentru meridianele de vest și de est. Pentru rezultate laturile build dimensiuni dreptunghi (foaie cadru interior), care va fi baza pentru construirea meridiane și paralele intermediare card, precum și pentru aplicarea punctelor de referință.
Meridiane și paralele Mercator reprezentate de linii paralele reciproc și perpendiculare, astfel încât construcția lor este suficientă pentru a defini segmentele D. Pentru paralele punctele de intersecție carte de meridianul cu axa X și ordonata la intersecția punctelor meridian harta pe axa Y. Atunci când aceste valori sunt găsite pentru a determina diferența D - Dyu și y - Y3 pentru punctele de mai sus. Aici Dyu - meridian secțiunea din sud-vest meridianul ordonatei paralele și înguste. Aceste diferențe pune pe primele cadre de sud-vest colț, pe laturile de vest și de sud și prin punctul de depunere se realizează linii paralele, respectiv laturile de sud și laterale, care vor fi paralele și meridiane card.
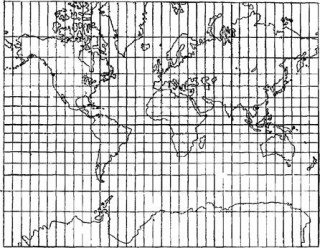
Figura 3 Maparea proiecția netă conformal cilindrică (Mercator)
Fig. 3 prezintă un reticul în proiecție cilindrică CONFORMAL (tangent la cilindrul) a imaginii globului. Valorile scalei în această proiecție sunt prezentate în Tabelul 4.
Scară în conformal cilindrice de proiecție Mercator.
Datorită faptului că proiecția Mercator este conformal și meridianele sunt reprezentate prin linii paralele în ea, are o linie de proprietate remarcabilă care traversează toate meridianele la același unghi, este descris în această linie de proiecție. Această linie se numește linie rombice. Mutarea cu barca, dacă se utilizează o busolă menține aceeași rată de fapt merge pe linia rombice. A spus proprietate Mercator a condus la utilizarea sa pe scară largă pentru diagrame nautice.
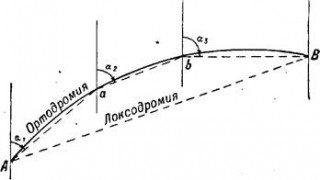
Fig. 4. Marele cerc și linia rombice pe hartă în proiecția Mercator
cerc Mare și linia rombice
Conform hărții trase în proiecție Mercator, mod ușor și simplu pentru a sărbători navei și de a determina cursul de echilibru, t. E. direcția în care trebuie să se deplaseze pentru a obține de la un punct la altul. curs permanent al navei se determină prin măsurarea unghiului de echer dintre linia care leagă aceste puncte de pe hartă, și unul dintre meridianele.
Cu toate acestea, trebuie remarcat faptul că în cazul în care distanța dintre punctele A și B (fig. 4), pe sfera loxodrome se îndepărtează în mod semnificativ departe de cercul mare (cea mai scurtă distanță între punctele), care proiecțiile
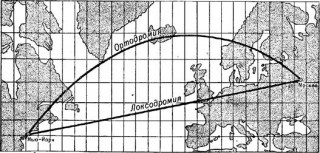
Fig. 5. Marele cerc și linia rombice între New York și Moscova, pe o hartă în proiecția Mercator.
Mercator este reprezentată printr-o curbă. În acest caz, navigatorul nu este pe de o rată de navă, și mai multe, direcția de schimbare în punctele specifice (a și b). Calea navei la aceeași părere pe hartă sub formă de linii rupte polifonice înscrise în cercul mare. Cu referire la desen, o navă din punctul A la punctul A trece sub azimutul de la punctul A la punctul b - sub azimutul punctului b la punctul final B - pentru azimut.
Pentru claritate, puteți specifica (figura 5.) că între New York și Moscova, lungimea cercului mare este 7507 km și linia rombice - 8371 km, adică diferența dintre lungimea lor este de 864 km ... Cele mai multe puncte de eliminare a loxodrome orthodromy de aici ajunge la 1650 km.
În al doilea rând comoditate Mercator în cererea sa de diagrame nautice este că face ușor, cu o precizie suficientă pentru scopuri practice, să fie determinat de harta distanța în mile marine, fără a recurge la construirea de cântare speciale, și folosind doar diviziunile (în grade sau minute), depuse pe laturile cadrului cardului. mile marine este egal cu 1.852 m, care corespunde aproximativ cu lungimea medie a arcului de meridianul de un minut.
Dacă, de exemplu, harta este necesar să se determine în mile marine distanța AB (Fig. 42), apoi eliminând segmentul soluție etrierului AB este aplicată divizorului cel mai apropiat cadrul lateral al cardului, astfel încât otrezka- punctul median C a fost pe lățimea medie a punctelor A și V (punctul C1). Numărul de minute meridianul numărate în cadrul acestui segment, și va exprima distanța în mile marine AB (Fig. 6 segment AB = 215 mile).
În concluzie, trebuie remarcat faptul că, în pregătirea hărților topografice și de supraveghere și topografice ale diferitelor scale sunt utilizate pe scară largă ca material de cartografiere hărți marine diferite compilate în proiecție cilindrică CONFORMAL. Prin urmare, cunoașterea caracteristicilor această proiecție este de mare importanță practică.
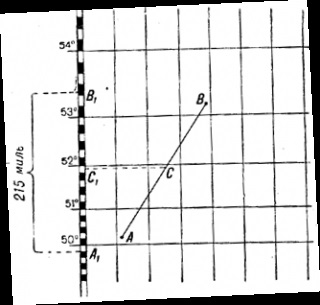
Fig. 6. Determinarea AB distanța în mile pe hartă în proiecția Mercator
Calculați segmentul D meridian și ordonata „y“ în proiecția conformal cilindric pe un cilindru tangent la coordonatele geografice = 30 °, 35 ° (de la medie meridian luate ca axa X) pentru k = 1: 5000000. Krasovsky elipsoidală.