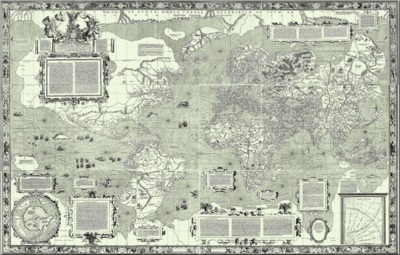
Mercator Harta Lumii 1569
Conformal cilindrice Mercator - una dintre principalele proiecții cartografice. Gerardom Merkatorom este proiectat pentru a fi utilizat în „Atlas“ lui. „Conformal“ în numele proiecției subliniază faptul că proiecția păstrează unghiurile dintre direcțiile. Toate linia rombice în ea sunt reprezentate prin linii drepte. Meridianele în Mercator reprezentate linii paralele echidistante. Aceleași paralele sunt linii paralele, distanța dintre care este aproape de ecuator este egală cu distanța dintre meridianele și crește rapid atunci când se apropie de poli. Polonezii înșiși nu pot fi reprezentate în Mercator (acest lucru se datorează particularităților funcție de reprezentare a coordonatelor pe sfera pe coordonate plane), deci este de obicei carte de regiuni limita Mercator la 80-85 ° latitudine nordică și sudică.
Scala de pe hartă în această proiecție nu este constantă, este crescut de la ecuator la poli (ca arccosinusul a latitudinii), dar gradul de verticale și orizontale sunt întotdeauna egale decât, de fapt, realizat proiecția CONFORMAL. Pe hărțile din această proiecție întotdeauna indicat, se referă la o scară mai mare paralelă a hărții.
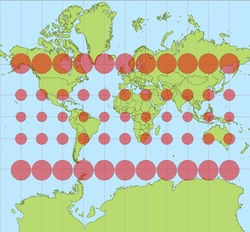
Denaturarea de spațiu în Mercator
Deoarece Mercator are o scară diferită la diferite site-uri, această proiecție nu păstrează zona. În cazul în care scara de bază se referă la ecuator, cea mai mare deformare de dimensiuni obiecte sunt la poli. Acest lucru se vede clar pe hărțile din această proiecție: ei cred că Groenlanda este de 2-3 ori mai mare în Australia și este comparabil ca marime in America de Sud. În realitate, Groenlanda este de trei ori mai mică decât Australia și de 8 ori mai mică decât în America de Sud.
Mercator a fost foarte convenabil pentru nevoile de navigare, mai ales în zilele vechi. Motivul este că traiectoria mișcării navei, venind în aceeași rumba la meridianul (adică, aceeași poziție a acului busolei pe scală) este reprezentată printr-o linie dreaptă pe hartă în proiecția Mercator.
Expresia matematică a proiecției Mercator
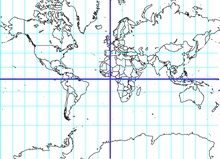
hartă a lumii într-o proiecție Mercator coordonatei liniile trasate prin 20 °.
În primul rând, ia în considerare cea mai simplă variantă a proiecției Mercator: proiecția sferei pe cilindru. Această opțiune ignoră aplatizare la polii Pământului. proiecție cilindricitate ne dă imediat o expresie pentru coordonatele orizontale de pe hartă: este pur și simplu proporțională cu longitudinea punctului # X03BB; (Atunci când este utilizat în calcule trebuie remarcat faptul că această cantitate trebuie să fie exprimate în radiani)
Stare conformality - este doar egalitatea în nivelul axei orizontale și verticale. Deoarece scara pe axa X la o latitudine # X03B8; Este pur și simplu egal cu c / (cos R # X2061; # X03B8; ) (R - raza Pământului), din cos R stare d y # X2061; # X03B8; / C = Rd # X03B8; obținem următoarea expresie pentru dependența y # X03B8;
Acum este ușor să se obțină expresii de proiecție conformist ținând cont de forma elipsoidala a Pământului. Pentru a face acest lucru avem nevoie pentru a scrie o valoare pentru o formă elipsoid (a - axa semi-majoră, b - minor) în coordonate geografice
mutați-l la coordonatele x și y, și echivala magnitudinea axelor. După integrarea obținem
x = c ( # X03BB; # X2212; # X03BB; 0) y = c [păcat t h # X2061; # X03B8; # X2212; # X03B5; un t h ( # X03B5; păcat # X2061; # X03B8; )]. x = c (\ lambda - \ lambda _) \\ y = c [>> \ păcat \ theta - \ varepsilon >> (\ varepsilon \ păcat \ theta)] \ end >>.
aici # X03B5; 2 = a # X2212; b 2 / a ^ -b >> / a> - excentricitatea elipsoid pământului. Conversia inversă este exprimată în termeni de funcții elementare, ci o ecuație pentru transformata inversă este ușor de rezolvat de teoria mică perturbație # X03F5; .
Formula iterativ pentru transformata inversă este următoarea:
# X03B8; n + 1 = f ( # X03B8; n. y) = f \ left (\ theta _ y \ dreapta)>. unde # X03B8; 0> poate fi luat egal cu 0 sau aproximativ calculat conform formulei pentru o sferoid. # X03B8; n + 1 = a r c s i n (1 # X2212; (1 + sin # X2061; # X03B8; n) (1 # X2212; # X03B5; păcat # X2061; # X03B8; n) # X03B5; e 2 y c (1 + # X03B5; păcat # X2061; # X03B8; n) # X03B5; ) = Arcsin \ stânga (1 -) (1 \ varepsilon \ păcat \ theta _) ^ >> (1+ \ varepsilon \ păcat \ theta _) ^ >> \ dreapta)>