Aceasta este prima pătrat magie, referindu-se la varietatea de pătrate așa-numitele diavolului.
Magic Quadrant Yan Hueya (China)
În secolul al 13-lea. matematician Yan Huey a preluat problema metodelor de construire patrate magice. Cercetarile sale a fost continuată apoi de alți matematicieni chinezi. Yan Huey considerate pătrate magice nu sunt doar a treia, dar ordinele mari. Unele dintre pătrate sale sunt destul de complexe, dar el a dat întotdeauna regulile pentru construcția lor. El a reușit să construiască un pătrat magic al șaselea ordin, acesta din urmă a fost aproape asociativă (există doar două perechi de numere opuse centrale nu dau un total de 37) [2]

Pătrate de origine europeană
Pătratul Albrehta Dyurera

gravuri Fragment Durer „Melancolie“
Magic Quadrant 4CH4, reprezentat într-o gravură Albrehta Dyurera „Melancolia I», este considerat a fi cel mai devreme în arta europeană. Două numere de mijloc din rândul de jos indică data creării picturii (1514).
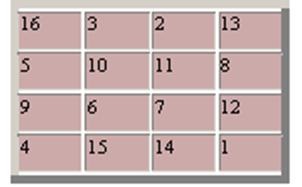
Suma numerelor în orice orizontală, verticală și diagonală egală cu 34. Această sumă se regăsește în toate colțurile pătrat 2CH2, în piața centrală (10 + 11 + 6 + 7), pătrat celulelor de colț (16 + 13 + 4 + 1), în pătrate construite "leagăn cal" (2 + 8 + 9 + 15 și 3 + 5 + 12 + 14), în dreptunghiurile formate din perechile de celule secundare pe laturile opuse ale (3 + 2 + 15 + 14 și 5 + 8 + 9 12). Cele mai multe dintre simetriile suplimentare asociate cu faptul că suma oricăror două numere de la nivel central, dispuse simetric este egal cu 17.
Pătrate Henry E. Dudeney și Allan W. Johnson -ml.
Dacă o matrice pătrată de n × n este înregistrată nu este strict numere naturale, atunci magia pătrat - neconvențional. Mai jos sunt două astfel de pătrate magice pline cu cele mai multe ori doar un număr. Primul este de ordinul n = 3 (pătrat Dudeney); a doua (dimensiune 4x4) - pătrat Johnson. Ambele au fost dezvoltate la începutul secolului al XX-lea
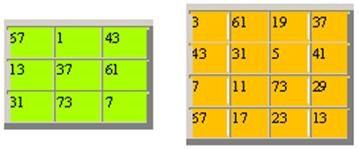
Există mai multe astfel de exemple:
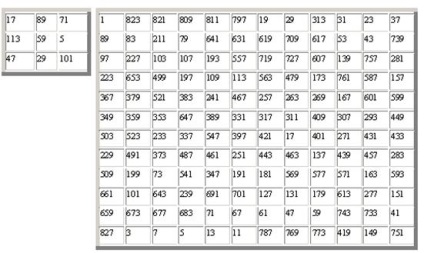
Ultimul pătrat este remarcabil prin aceea că acesta este compus din 143 de numere prime consecutive, cu excepția a două lucruri: unitatea în cauză, care nu este un număr prim, și nu sunt folosite doar un prim chiar numărul 2.
pătrat magia Diavolului
Devil Magic pătrat - pătrat magic, care coincide, de asemenea, cu suma constantă magică a numerelor de diagonală rupte (diagonală, care sunt formate prin plierea unui pătrat în torr), în ambele direcții.
Aceste piețe sunt numite mai pandiagonalnymi.Suschestvuet 48 4CH4 pătrate magice diabolice până la rotații și reflecții. Dacă luăm în considerare mai multe și mai simetrie - traduceri paralele torice, atunci nu va fi doar 3 pătrat în mod semnificativ diferite:
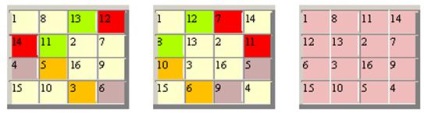
Cu toate acestea, sa dovedit că ultima opțiune a treia este pur și simplu permutări de numere obținute prin primele două pătrate. Aceasta este a treia opțiune - este un pătrat diabolica de bază, din care diferitele transformări se pot construi tot restul.
pătrate Pandiagonalnye sunt pentru ordine impar n> 3, în orice paritate dublă comandă n = 4k (k = 1,2,3 ...) și nu există pentru o singură paritate ordinul n = 4k + 2 ().
pătrate Pandiagonalnye de ordinul al patrulea au o serie de proprietăți suplimentare pentru care acestea sunt numite perfecte. pătrate perfecte de ordin ciudat nu există. Dintre pătratele pandiagonalnyh dubla paritate peste 4 sunt angajate. [2]
pătrate Pandiagonalnyh cincea ordinul 3600. Având în vedere traducerile paralele torice are 144 pătrate pandiagonalnyh diferite. Unul dintre ele este prezentat mai jos.
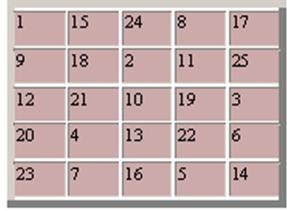
Rupt diagonală pandiagonalnogo pătrat
Dacă pătrat pandiagonalny este de asemenea asociativ, este numit un ideal. Un exemplu de magie pătrat perfectă:
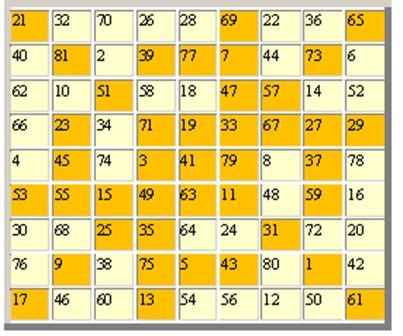
Originile pătratului magice sunt pierdute în Evul Mediu. Istoria patrate magice este indisolubil legată de dezvoltarea științei. Cu toate acestea, în cazul în care în cele mai vechi timpuri piața de interes a fost mai mult decât un ezoteric, care în prezent un pur practic. Folosind algoritmi umple patrate magice ar rezolva unele probleme de criptografie. De asemenea, a constatat existența unei piețe de umplere parțială a algoritmilor magice. Algoritmul general potrivit pentru toate tipurile de pătrate magice există.