V. Luați în considerare setul format din puncte legate într-un fel. Elemente - colțuri. GrafG = G (V) cu setul de vârfuri V este o familie de combinații sau perechi de forma
indicând care nodurile sunt considerate conectate.
În conformitate cu reprezentarea geometrică a graficului, fiecare pereche particular se numește o muchie (arc) în grafic, și - punctul final.
Puteți defini noțiunea de grafic în caz contrar, dacă ne imaginăm un set de puncte numite noduri V. plan. și o multitudine de segmente directionale E, conectarea toate sau unele dintre varfuri si numite arce. Ie matematic graficul G poate fi definit ca o pereche de seturi G = (V, E). Exemple de grafului poate fi o hartă de drumuri sau căi ferate, un circuit compus circuitelor electrice, etc.
Putem presupune că o multitudine de arce direcționate care leagă elementele E. V. pluralitate de afișare este setat în sine. Prin urmare, putem presupune specifica graficului, în cazul dat setul de vârfuri V și o metodă pentru afișarea unei multitudini V T în V. Astfel, graficul G este o pereche (V, T), constând dintr-o multitudine de V T și afișa dat pe acest set.
De exemplu, Fig. 2.1 prezintă un grafic ale cărui vârfuri sunt punctele a, b, c, d, e, g, h, și arce - segmentele (a, a), (c, b), (c, d), (c, e), (d, c), (d, d), (e, d), (g, h). Se afișează graficul redus va fi definită după cum urmează: T a =; T b =Æ; T c =; T = d; T e =; T = g; T h =Æ.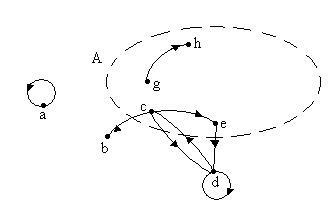
Este ușor de observat că această definiție a graficului este identică cu definiția relației pe platoul de filmare.
Din cele de mai sus se poate stabili că graficul G (V, E) este un set de două seturi - un set nevid V (set de noduri), iar setul E de subseturi sale elementului dublu de V (E - o multitudine de nervuri).
În definiția marginilor pot fi luate sau nu sunt luate în considerare ordinea celor două capete ale lui. Dacă această comandă nu este esențială, și anume în cazul în care. E este marginea neorientat, iar dacă ordinul este semnificativ, atunci D se numește o margine direcționată, și în care vi fi vertex inițial, - vertexul final.
Un grafic se numește orientat. Dacă se concentreze toate marginile sale.

graf neorientat este un grafic direcționat
În unele cazuri, există un grafice mixte.
Ca și în cazul nervurilor orientate și neorientate spun că muchia E = (vi. Vj) este incident de la vi vârfuri și vj și că nodurile vi și marginea vjintsidentny E. Cele două vârfuri incidentul numit adiacente o margine. Vertex nu incident de la orice margine se numește izolat. Adesea are sens să ia în considerare numai partea de sus non-izolate.
Numărul muchiilor incidente vertexul u este numit vertexul grad și deg denotat (u).
Grafic constând numai din vârfuri izolate, numite graficul nul.
Cel mai important caz este plin grafG = (V, E), ale cărei margini sunt toate perechile posibile de () pentru două vi vârfuri diferite și vj ale V. Graficul complet cu noduri indicate. Fig. 2.3 prezintă totalul contează și, respectiv.
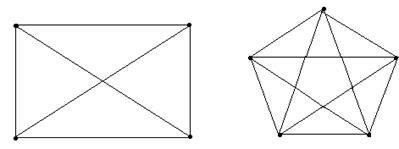
Graficul complet sunt perechi de muchii, câte una în fiecare direcție care leagă oricare două vârfuri vi și vj distincte orientate. Nervurile, în care ambele puncte finale coincid L = (a, a) se numește buclă.
(A se vedea. Fig. 2.1 partea superioară "și", "d"). Bucla este de obicei considerat a fi neorientate. Poate fi extins la un grafic complet al graficului complet cu bucle, adăugați o buclă la fiecare nod.
Se presupune că nodurile pereche conectează mai multe coaste diferite.
Pentru fiecare grafic direcționat un grafG invers *. schimbarea care rezultă în orientarea fiecăreia dintre marginile graful G este inversată.
Pentru fiecare grafic direcționat, există, de asemenea, un grafGu neorientat asociat. marginile sunt marginile G., dar fără orientare. Uneori este convenabil să transforme un grafic G neorientat într-un grafic dirijat Gd prin procedeu care constă în înlocuirea fiecărei nervuri G pereche de nervuri cu aceleași picuri și atribuindu-le (margini) de orientări opuse dublare.
Un grafic se numește plat dacă se poate demonstra în planul, astfel încât toate muchiile sunt nodurile intersecția G.
grafice regulate. Graf este regulat sau uniform dacă toate nodurile sale au același grad exact. În cazul în care gradul de fiecare nod este egal cu k. atunci graficul este numit un grafic regulat de gradul k. De exemplu, un grafic complet de ordinul n-lea este un grafic obișnuit de grad k = n-1. De exemplu, clasa regulate 3 grafice numite grafice cubice sau 3-valent. Ca un exemplu, în Fig. 2.4 este un grafic cubic Petersen.
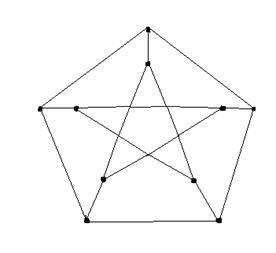
grafice platonice. Grafic platonic este un grafic format de vârfurile și muchiile cinci poliedre regulate - solidele platonice: tetraedrul, cubul, octaedru, dodecaedrul, icosaedru.
grafice bipartite. Un grafic se numește bipartit dacă există o partiție de vârfuri sale în două clase, în care capetele fiecărei nervuri sunt în diferite clase.
PodgrafomGA graf G = (V, T) este un grafic care include numai o parte G din nodurile care formează mulțimea A, împreună cu arcurile care conectează aceste noduri. De exemplu, regiunea conturată punctată din Fig. 2.1. Matematic, acest lucru este scris după cum urmează:
Parțial grafic HG cu privire la graficul G = (V, T) este un grafic care conține numai o parte a arcelor grafului G. adică definit de condiția
De exemplu, dacă G = (V, T) - România harta drumurilor, apoi harta rutieră zona Nijni reprezintă subgraful și principalele autostrăzi carte de Romania - graficul partial.
Prin intermediul unui grafic G se numește o secvență de arce d = (u1. U2. ... uk), în care capătul fiecărui arc anterior coincide cu începutul următorului. Calea d. vârfuri succesive sunt noduri a, b, c, ... m este notat cu d = (a, b, c, ... m).
Putid lungime = (u1. U2. ... uk) este numărul l (d) = k, egal cu numărul de arce care alcătuiesc calea d. Uneori, fiecare arc este creditat ui cu un număr l (ui), numită lungimea arcului. Apoi, lungimea traseului este definită ca suma lungimilor arcelor care formează calea
Modul în care nici un arc are loc de două ori, este numit simplu. Modul în care nici un nod apare de două ori, se numește elementar.
Circuit - o cale (v1 v2 ... vk ..) d = finală, în care nodul inițial coincide cu x1 vk final. Când acest circuit se numește un elementar dacă toate nodurile sale sunt diferite (cu excepția celor pentru începutul și sfârșitul, care coincid). unitatea de circuit de lungime formată sub formă de arc (a, a) se numește buclă. De exemplu, în Fig. 2.1 (e, d, c, b) - calea (c, e, d, c) - buclă, (d, d) o buclă.
Pentru un graf neorientat, respectiv și a introdus bucla lanț concept. Lanț (ciclu) se numește Euler. în cazul în care trece prin toate marginile o dată. Circuit (ciclu) este hamiltonianul. în cazul în care trece prin toate nodurile graficului dată.