Prin punctul P și diametrul cercului efectuat două acorduri
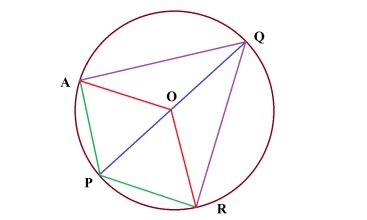Sarcină. Prin punctul P a avut loc circumferential diametru PQ și două acorduri
PA și PR sunt egale cu raza cercului.
Găsiți unghiurile de patrulater măsuri și gradul de PR PRQA arcelor, RQ, QA, AR.
Soluție: Desenam un cerc, țineți PQ - diametrul și coarda în ambele direcții
de la P - PR și PA.
Patrulaterul PRQA unghiurile R și A sunt egale cu 90 de grade,
colțuri, cum ar fi inscriptionate care se sprijină pe un diametru.
Cercul punct central O este conectat la toate nodurile
și ia în considerare triunghiul OPR.
Ea toate laturile egale cu raza unui cerc - PO și OR - raze, PR - coardă, cu condiția de rază egală, adică este un triunghi echilateral.
Într-un triunghi echilateral toate unghiurile sunt 60º.
Prin urmare, unghiul central de POR, de asemenea, egal cu 60º.
Rezultă de aici că arc PR, pe care se bazează,
Are gradusnuju măsoară 60 °.
De asemenea, puteți lua în considerare un triunghi AOP și a vedea
că arcul AP are, de asemenea, gradusnuju măsoară 60 °.
Egalitatea unghiurilor într-un triunghi echilateral, putem concluziona că unghiul DAE este egal cu suma dintre cele două unghiuri - APO și RPO,
și anume Este 120º.
Prin urmare, Q Unghi patrulater este 180-120 = 60º. Conform teoremei, care prevede că suma unghiurilor opuse ale unui patrulater înscris într-un cerc este egal la 180 °.
Rămâne de a determina PQ arcelor măsură de gradul și AC. Acesta poate fi calculat prin luarea în considerare triunghiuri și AOQ ROQ.
Aceste triunghiuri sunt isoscel, deoarece AO = QO = RO = raza cercului.
Unghiuri aceeași AOQ ROQ și egale în 120º, ambele adiacente AOP'ul colțuri și POR, care sunt egali în 60º.
Acest lucru arată că AQ și RQ au un grad de arc măsoară dimensiunea 120º.
A: Unghiurile de patrulater R, Q, A, P egal cu 90º, 60º, 90º, 120º.
arce de ieri măsuri: 60º, 120º, 120º, 60º.
De asemenea, ar putea fi interesat:
- AU baza unui triunghi isoscel este egală cu 12
- Exemplele 7 clasă de geometrie.
- Dovezi clasa geometrie 7.
