În primul rând, vectorii sunt coliniare. Doi vectori se numesc coliniare. în cazul în care se află pe aceeași linie sau linii paralele. Aproximativ vorbind, vorbim despre vectori paralele. Dar, în ceea ce le folosiți întotdeauna adjectivul „coliniare“.
Imaginați-vă doi vectori coliniare. Dacă vectorii săgeată de date sunt îndreptate în aceeași direcție, astfel de vectori sunt numite codirectional. În cazul în care săgețile sunt în căutarea în direcții diferite, atunci vectorii sunt îndreptate în sens opus.
Legendă: vectori coliniare scrie paralelism icon familiar :. în care detaliază: (vectori colineare) sau (vectori) direcționate opus.
Produsul a numărului de vector nenul este un vector. a cărui lungime este egală. Mai mult, vectorii și sunt coliniari cu și oppositely îndreptate cu.
Regula vector de înmulțire cu un număr este mai ușor de înțeles cu ajutorul desenului:
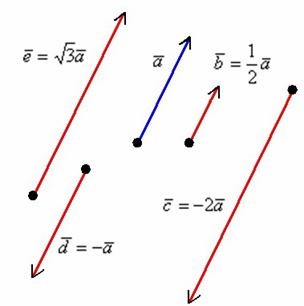
vectori 9.Kollinearnye și coplanare
Definiția. Vectorii sunt numite coliniare. în cazul în care acestea sunt pe aceleași linii paralele sau. Vectorul de zero este coliniar cu orice vector. \
Definiția. Vectorii se numesc coplanari. în cazul în care există un plan, ei întotdeauna vectori parallelny.Kollinearnye sunt coplanare, dar nu toate coplanare vectori coliniare.
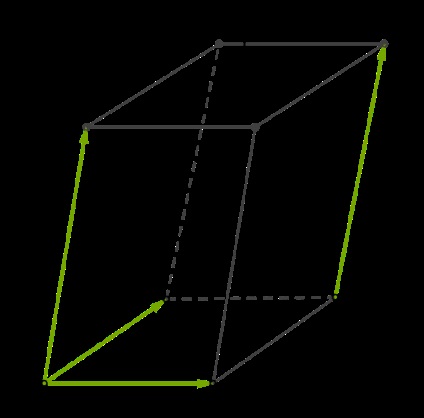
Toate cazurile de mai sus este ușor să ia în considerare, dacă ai pus vectorii pe marginile cutiei.
1. Orice doi vectori sunt în același plan, dar, în același plan poate fi plasat și vectori AA1- → -, CC1- → - și AD- → -, adică vectorii sunt coplanare. De asemenea, coplanare vectori AA1- → -, AB- → - și CC1- → -, deoarece doi dintre acești vectori sunt paralele. Este ușor de imaginat că, dacă le aduce la o origine comună, vectorul CC1- → - coincide cu vectorul AA1- → -.
2. De exemplu, vectorii ab- → -, AD- → - și AA1- → - nu coplanare, deoarece acestea nu pot fi plasate în același plan.
Simptom coplanarității trei vectori:
Să vectorii o # 8407; și b # 8407; Nu coliniar. Dacă vectorul c # 8407; există doar o pereche de numere reale x și y, cum ar chtoc # 8407; = X # 8901; a # 8407; + Y # 8901; b # 8407;. atunci vectorii o # 8407;. b # 8407; și c # 8407; coplanare.
Reciproca deține, de asemenea:
În cazul în care cei trei vectori o # 8407;. b # 8407; și c # 8407; vectori coplanare și # 8407; și b # 8407; nu coliniare, vectorul c # 8407; poate fi extins în ceea ce privește vectorii un # 8407; și b # 8407; un singur mod.
10. Coordonatele punctului coordonatele vectorului
În cazul în care sunt date două puncte, iar avionul. vectorul are următoarele coordonate:
Având în vedere două puncte în spațiu și. vectorul are următoarele coordonate:
Aceasta este, de la sfârșitul coordonatele vectoriale, scădeți coordonatele corespunzătoare ale începutului vectorului.
Asigurați-vă că pentru a înțelege diferența dintre coordonatele punctelor și coordonatele vectorilor:
Coordonatele punctelor - acestea sunt coordonatele obișnuite într-un sistem de coordonate cartezian. Amânați punctul de pe planul de coordonate, am toată lumea poate încă 5-6 clasă cred. Fiecare punct are un loc strict în avion, și mutați-le în altă parte este imposibil.
Coordonatele vectorului - este expansiunea în bază. în acest caz. Orice vector este gratuit, deci, dacă aveți nevoie putem amâna cu ușurință de la un alt punct al planului. Interesant, pentru vectorii este posibil să nu se construiască coordona un sistem de axe rectangulare are nevoie doar de bază, în acest caz, o bază ortonormală a planului.
Înregistrarea coordonatele punctelor și coordonatele vectorilor par a fi similare :. și coordonează înțelesul complet diferit. și aveți nevoie de o bună înțelegere a diferenței. Această diferență, desigur, adevărat pentru spațiu
11.Koordinaty sumă și diferență de vectori, produsul numărului de
Adăugarea de vectori (suma vectorială) a + b este operația de calcul a vectorului c, ale cărei elemente sunt suma pairwise elementelor corespunzătoare ale vectorilor a și b, adică, fiecare element vector c este egal cu: ci = ai + bi
Substracție vectorilor (diferența vector) a - b este operațiunea de calcul a vectorului c, ale cărei elemente sunt diferențe pereche ale elementelor corespunzătoare ale vectorilor a și b, adică, fiecare element al vectorului c este dată de: ci = ai - bi
În cazul sumei problemei spațiului și diferența vectorilor a = x; ay; az> și b = x; prin; bz> pot fi găsite folosind următoarele formule: