ipoteză
Birch - Swinnerton-Dyer
În timp ce nu a fost găsit nici un model care descrie distribuția numerelor prime printre naturale, Riemann a constatat că numărul de numere prime. care nu depășește x, - funcția de prim-numărare. notat # X03C0; (X) - exprimat în termeni de distribuție a așa-numitei „zerouri banale“ funcția zeta.
Multe dintre acuzațiile de distribuire a numerelor prime, inclusiv complexitatea computațională a unor algoritmi întregi. a demonstrat ipoteza de loialitate a ipotezei Riemann.
formulare
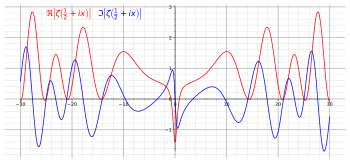
Real (roșu) și (albastru) componente imaginare ale funcției zeta
Din ecuația funcțională # X03B6; (S) = s 2 # X03C0; s păcat # X2061; # X03C0; s 02 ianuarie păcat # X2061; # X03C0; s # X0393; (S) # X03B6; (1 # X2212; s) \ pi ^ \ păcat> \ zeta (1-s)> 1, și expresia explicită # X03B6; (S) = # X2211; n = 1 # X221E; # X03BC; (N) n s> = \ sum _ ^ >>> dacă Re s> 1 \, s> 1>. unde # X03BC; (N) - funcția Mobius. rezultă că toate celelalte zerouri, numite „non-triviale“, situat în banda 0 # X2A7D; Re s # X2A7D; 1 \, s \ leqslant 1> simetric față de așa-numita „linia critic» 1 2 + i t. T # X2208; R + l, \; t \ în \ mathbb>.
Ipoteza Riemann
Ipoteza Riemann afirmă că:
„Toate zerouri non-triviale ale funcției zeta au parte reală egală cu 1 2 >>“
că este, numere complexe sunt situate pe linia Re s = 1 2 >>.
Generalizat Riemann Ipoteză
Generalized Riemann Ipoteză (Eng. Generalized Ipoteza Riemann) este de aceeași aserțiune pentru generalizarea zeta funcții, numite Dirichlet L funcții.