Numărul de identificare Informregistr: 0420600020 \ 00
În prezent, există diferite teorii de proporții, care a fost însoțită de arhitectura în toate etapele istoriei sale. Esența toate proporțiile conceptelor - stabilirea unui ordin legitim, care poate determina compoziția la unitate și armonie.
Introducerea oricăror tipare (numeric, geometrice), legate de conceptul de diferite tipuri de simetrii (statice, dinamice, etc).
Articolul discută teoria design arhitectural, fiind construit pe baza dublei pătrat, permițând scăpa de proporții disparate.
efect artistic compoziții simetrice clasice se datorează adevărata construcție a modulului. Oamenii reacționează nervos la clădirea care par grele dezechilibrată sau de top. Și nu pentru că pot cădea pe noi, ci pentru că oamenii sunt mental, deoarece însuși proiectat pe construirea propriului său corp se corelează cu construirea corpului. mușchii noastre dureri atunci când văzut cornișă grele, mușchii tensionate în simpatie atunci când un dezechilibru este detectat în compoziția arhitecturală. Așa-numitul instinct mimetic inconștientă ne face să asimileze ei înșiși greutate aparentă, presiune, rezistență, prezentate în forme care sunt văzute și anume cu alte cuvinte, există conceptul de „vzhivaemosti“ în structura clădirii.
Cu conceptul de relativă egalitate atrage după sine înțelegerea modele geometrice, în cazul în care acesta poate fi împărțit fără rest în părți egale în ceea ce privește o caracteristică geometrică, de exemplu, metoda de construcție. Înregistrarea modele geometrice pot fi efectuate sub forma unor numere sau formule.
Proporții diferite ale teoriei arhitecturii, însoțită în toate etapele istoriei sale. Esența tuturor conceptelor proporții - în ordinea stabilită de legi, ceea ce poate determina compoziția la unitate și armonie. Noțiunea de orice legi, numerice sau geometrice, incluse în conceptul de simetrie. Bazat pe conceptul de modele geometrice, putem construi conceptul de simetrie „dinamic“. Pentru o bază de simetrie statică selectată forma geometrică corectă. Este cunoscut faptul că raportul dintre laturile lor sunt reprezentate de numere raționale și relația irațională a elementelor lor sunt construite pe diagonala unui pătrat (V - 2) și latura sa (unitate). Astfel dreptunghi este construit cu zona V - 2. Apoi, pe diagonală și latura dreptunghiului original este construit dintr-un pătrat V - 3 etc. (Fig.1).
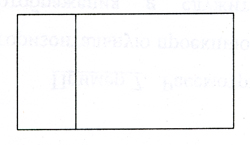
Fig.1. - dinamic dreptunghiuri
Această construcție poate fi continuată ad infinitum.
Aria dreptunghiului V - 5 servește ca bază cel mai bun exemplu de simetrie dinamică.
Teoria designului arhitectural în orice moment, este foarte important. De exemplu, la determinarea înălțimii spațiului boltit este utilizat numai aspect ratio aritmetică, geometrică și media. Să ne amintim, așa cum este determinat prin aceste mijloace. Numerele de secvență a1. a2. a3. a4 ... a numit-o progresie aritmetică. dacă diferența dintre orice număr și următoarele constante: a2 - a1 = a3 - a2 = a4 - a3 = .... De exemplu, numerele 1, 3, 5, 7, 9 ... formează o progresie aritmetică. In orice progresie aritmetică a3 = a1 + 2a2. a2 + a4 = 2a3, ... etc. Deci, cu alte cuvinte, fiecare număr este egal cu jumătate din suma numerelor adiacente. Fiecare membru al progresiei aritmetice se numește media numerelor adiacente. Astfel, obținem o regulă pentru calcularea mediei aritmetice a numerelor din două cifre a și b. care este egală cu: (a + b) / 2.
În cazul în care o secvență de numere a1. a2. a3. ... a4 are proprietatea că orice membru al relației cu secvența anterioară este în mod constant a2 / a1 = a3 / a4 = a2 / a3 .... o astfel de secvență este numită o progresie geometrică. În acest caz, a1 = a3 x (a2) 2. a2 = a4 × (a3) 2. ... astfel încât fiecare membru al unei progresie geometrică este rădăcina pătrată a produsului a două numere adiacente și media geometrică a două numere a și b calculat prin formula V - ab .
Numerele de secvență a1. a2. a3. ... a4 se numește progresia armonică. în cazul în care numerele de secvență, date de inversul 1 / a1. 1 / a2, 1 / a3. ... formează o progresie aritmetică. Orice membru al unei astfel de secvențe se numește o medie armonică a doi membri adiacenți, cu toate acestea, în scopul de a găsi o medie armonică a două numere a și b. în primul rând găsi media aritmetică a inversele de numere, și apoi inversul acestei medii. Astfel, media armonică este egal cu: 2ab / (a + b).
Pitagora a fost primul care a observat că terenul este emis de un șir strâns, de obicei, proporțională cu lungimea șirului. Dacă trageți șir întinsă, apoi apăsați degetul mijlociu și trage din nou, apoi tonul emis de către șirul pentru a doua oară, va fi o octavă mai mare decât prima. Dacă apăsați șirul și să fluctueze doar o treime din lungimea sa inițială, frecvența emisă de tonul ei este de trei ori mai mare decât frecvența fundamentală. Prin urmare, este clar cât de importantă secvență armonică formată de către membrii reciproce ale unei progresii aritmetice. Desigur, cele mai simple secvențe armonică are forma 1, 1/2, 1/3, 1/4, ...
O alta teorie a design arhitectural se bazează pe un pătrat dublu.
Două pătrate, stivuite împreună pentru a forma un pătrat dublu. Adăugarea celor două pătrate duble, vom găsi pătrat, repetând pătrat forma sa originală. Aceasta este o simplă proprietate de aditiv pătrat este utilizat pe scară largă în arhitectura Renașterii.
„Secțiunea de Aur“ a fost cunoscut arhitecți ai Renașterii, dar ei nu-l folosească în mod eficient ca un instrument pentru a obține proporții. „Aur Secțiunea“ Luca Pacioli numit proporția divină. Termenul „secțiunea de aur“ are originea în Germania, în prima jumătate a secolului al XIX-lea. și este dată de
m = (1 + V - 5) / 2