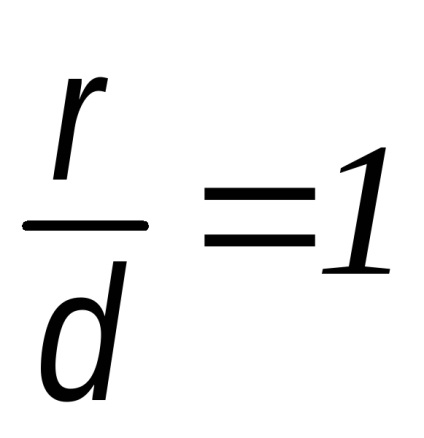Definiția. Un hiperbolă este locul geometric al punctelor de diferență de fiecare dintre acestea sunt două puncte de date este constantă numite focarele
Ia-un sistem de coordonate, astfel încât accentul pune pe axa x, iar segmentul partajat origine F1 F2 în jumătate (Fig. 30). Notăm F1 F2 = 2c. Apoi F1 (a, 0); F2 (-c; 0)
M
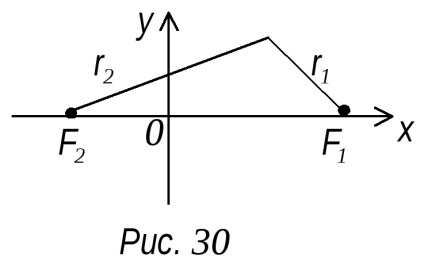
Conform definiției unui r1 hiperbolă - r2 = const.
Notam 2a
=> Ecuația canonică a hiperbola
Deoarece ecuația hiperbolă x și y în chiar puteri, în cazul în care punctul M0 (x0, y0) este pe o hiperbolă, atunci se află, de asemenea, M1 (x0, y0) M2 (-x0; y0) M3 (-x0; y0).
În consecință, hiperbola este simetrică în raport cu ambele axe.
Când y = 0 x 2 = 2 și x = ± a. nodurile hiperbolă sunt punctele A1 (a, 0); A2 (-a, 0).
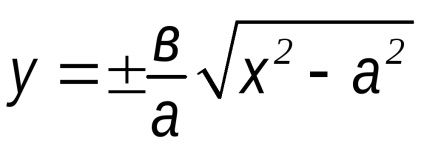
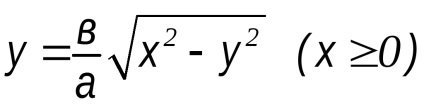
1)
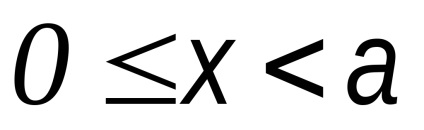
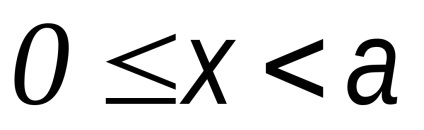
2) la x = a; y = 0 A1 (a, 0) aparține hiperbola
3) când x> a; y> 0. Mai mult decât atât, în creștere nelimitată hiperbolă ramură x merge la infinit.
Rezultă că o hiperbolă este o curbă care constă din două ramuri fără sfârșit.
6. asymptotes P unui hiperbolă
Luați în considerare împreună cu ecuația
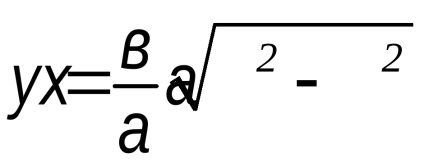
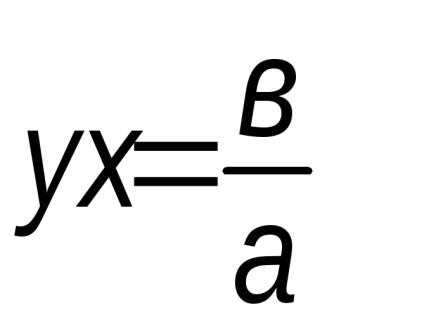
K
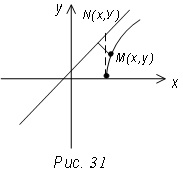
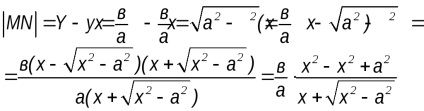
Deci, în cazul în care punctul M, se deplasează pe o hiperbolă în primul trimestru este îndepărtat la infinit, distanța de la linia
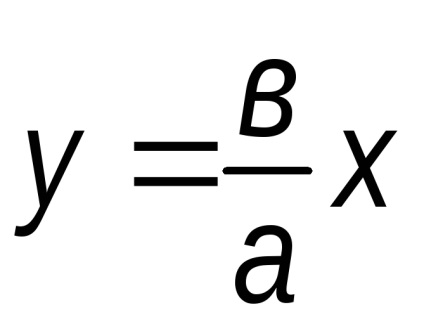
Prin simetrie, același lucru este valabil și pentru o directă
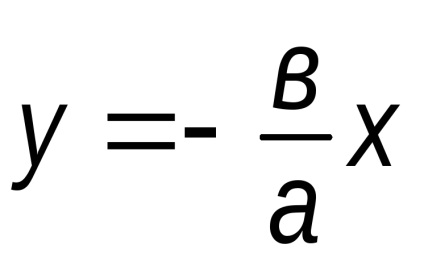
Definiția. Direct la care, la
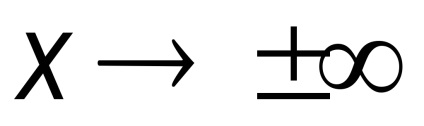
și
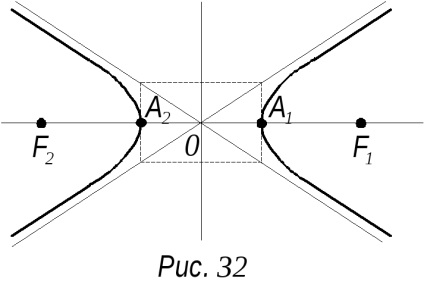
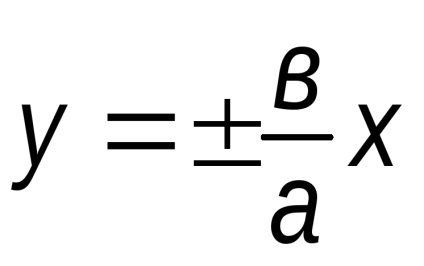
asymptotes hiperbolă sunt aranjate de-a lungul diagonalelor dreptunghiului, dintre care o parte este paralelă cu axa Ox și egalează 2a, în timp ce cealaltă paralelă cu axa Oy și egală cu 2c, iar centrul se afla la originea (Fig. 32).
N 7. Excentricitatea și hiperbolă directricea
r2 - r1 = ± 2a + semnul se referă la dreptul filialei hiperbolă
mark - se referă la ramura stângă a hiperbola
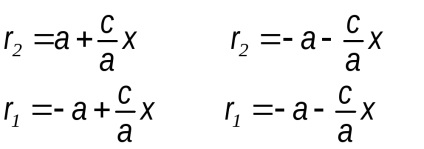
Opredelenie.Ekstsentrisitetom hiperbolă este raportul dintre distanța dintre focarele hiperbola și distanța dintre nodurile sale.
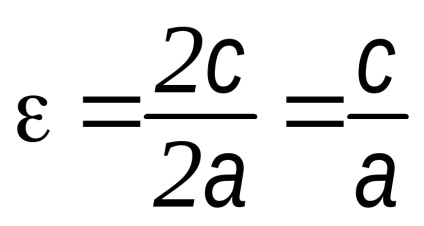
Ne exprimăm razele focale prin excentricitatea hiperbolă:
Definiția. Numim directă
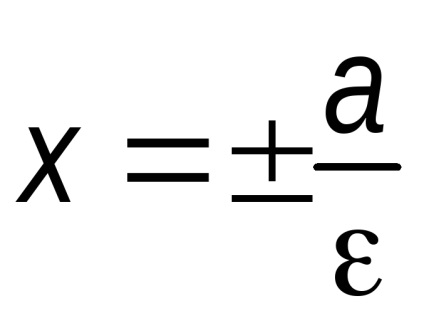

T
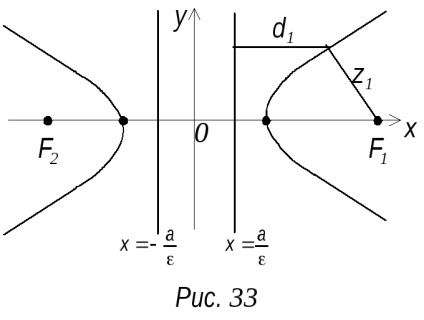
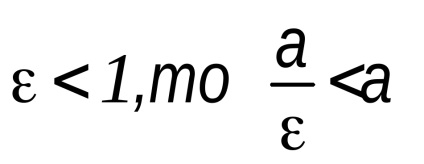
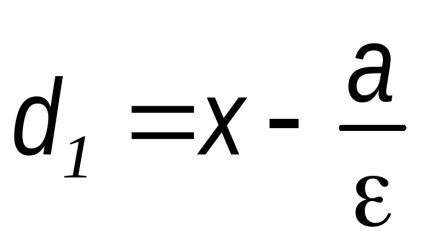
P. 8 și ecuația lui parabolei
oh
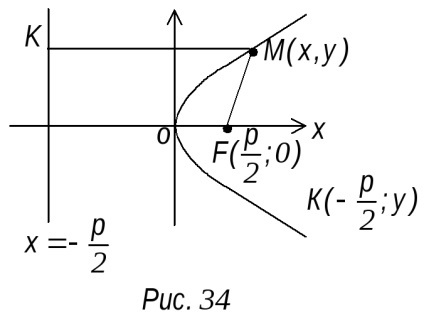
Pentru a face ecuația parabolei este luată ca axa x este linia care trece prin focalizare F1 perpendicular pe directoarei și presupun că axa x este dirijată de directoarei să se concentreze. După cum originea O ia mijlocul segmentului din punctul F la linia dată, a cărei lungime este notat cu p (Fig. 34). Cantitatea P va fi numit un parametru al parabolei. se concentreze coordonatele punctelor
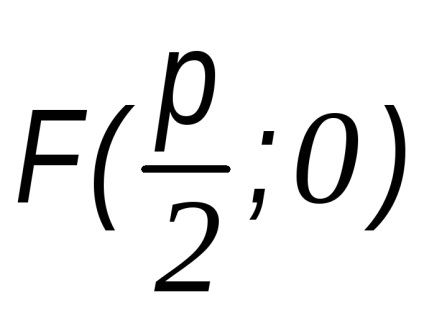
Fie M (x, y) - un punct arbitrar al parabolei.
v2 = 2px - ecuația canonică a unei parabole
Pentru a determina forma unei parabole transforma ecuația lui
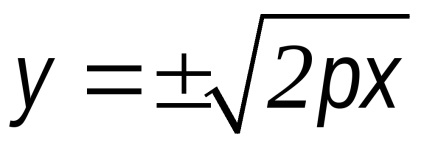
în
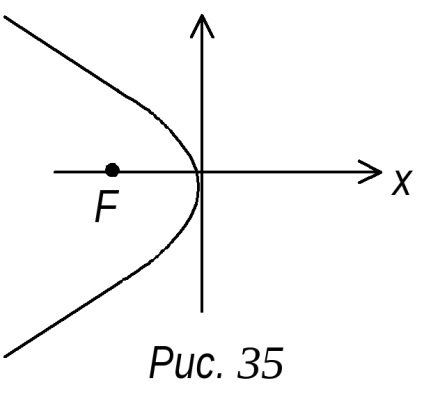
x
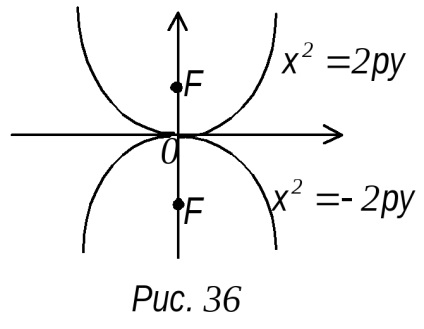
La o axă de simetrie a parabolei.
Dacă x este prima putere și y al doilea, care este axa de simetrie x.
Dacă x gradul al doilea, și la început, axa de simetrie este axa y.
Notă 1.Uravnenie parabole are Directoarea forma
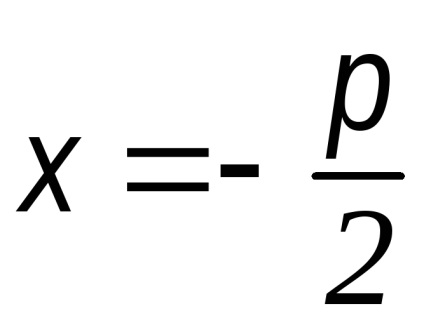
Notă 2.Tak pentru parabole