Tema. Sinus, cosinus, tangenta unghiuri de la 0 ° la 180 °
Scop: formarea conceptelor sinus, cosinus, tangenta unghiuri de la 0 ° la 180 °. Formarea abilităților de a găsi funcțiile trigonometrice unghiuri obtuze.
Tipul de lecție: combinate.
Vizibilitate și echipamente: Masa „Relația dintre laturile și unghiurile unui triunghi“ [13].
nivelul elevilor de formare necesită explica ce sinus, cosinus, tangenta unghiuri de la 0 ° la 180 °.
I. etapă organizațională
Deschiderea remarci de către profesor. Vom continua să studiem geometria. În clasa a noua, veți face cunoștință cu noua ramura a geometriei: triunghiuri de decizii arbitrare; poligoane regulate; coordonate carteziene în planul; transformări geometrice; vectori pe un plan; o introducere a geometriei solide. În fața ta sunt în așteptare pentru noi teoreme despre proprietățile forme geometrice, sarcini interesante.
Aș vrea să depășească obstacolele care stau în geometrie modul labirinturi. Lăsați studiul geometriei vă va aduce bucuria de a obține victorii.
II. cunoștințe de sprijin Cedl
Pentru a repeta informația despre funcțiile trigonometrice ale unghiurilor acute ale unui triunghi dreptunghic, puteți utiliza tabelul de beneficii. [13]
1. Formulați definiția cosinus, în unghi-tangenta triunghi unghi sinus, ascuțit.
2. Uita-te pentru orez. 1 sin α, cos α, tg α, β cos, β sin, tg β.
3. Ca α sin legate și cos α. în cazul în care a - un unghi ascuțit al unui triunghi dreptunghic?
4. Simplificarea expresia:
a) 1 + sin 2α + cos 2α;
b) 2 cos 2cx + 2α păcat - 1.
5. Ce fel de dependență legată sin α, cos α, α tg?
6. Localizați tg α, unde:
a) sin a =. cos α =;
b) sin a =. cos α =.
7. Setați valoarea expresiilor:
a) sin 30 °, 30 ° cos, tg 30 °;
b) sin 45 °, 45 ° cos, tg 45 °;
a) sin 60 °, 60 ° cos, tg 60 °.
III. Percepția treptată și conștientizare a noului material
Determinarea unghiurilor sinus, cosinus și tangenta de la 0 ° la 180 °
Studiu de material nou se poate face acest lucru. Construim un cerc cu centrul în origine și raza de 1 (fig. 2). Acest cerc se numește unitate. Construim un unghi ascuțit și care formează un cerc de rază OA cu direcția pozitivă a axei Ox. Lăsați punctul A are coordonatele (x; y). Apoi, în unghi drept triunghi AOB, avem:
Astfel: sinus unghiului a este ordonata punctului al cercului unitate, OA raza definește direcția pozitivă a unghiului axei Ox a. Cosinusul unghiului a este abscisa punctului al cercului unitate, OA raza definește direcția pozitivă a unghiului axei Ox a. Tangenta unghiului a este raportul dintre ordonata punctului A la abscisa punctului unde raza OAutvoryuє direcția pozitivă a unghiului axei Ox a.
Găsirea valoarea sinus, cosinus și tangenta unghiuri obtuze
Folosind definițiile furnizate, vom defini pentru orice unghi α, 0 ° α 180 °. Apoi, sin 0 ° = 0, cos 0 ° = 1, tg 0 ° = 0; păcat 180 ° = 0, cos 180 ° = - l. tg 180 ° = 0.
Dacă unghiul a - (. Figura 3) boante (0 ° α 90 °), ordonata punctului A este pozitiv (adică păcatul α> 0), abscisei - negativ (adică cos alfa 0), iar raportul între ordonata și abscisa - negativ (adică tg α 0).
În consecință, cosinus, tangenta unghiului obtuz negativ.
Dacă α - (. Figura 4) un unghi obtuz, apoi cos α = OS = - = OD - cos (180 ° - α),
păcat α = AC = AD = sin (180 ° - α), apoi tg α = = - = - tg (180 ° - α).
Deci, pentru a găsi sinusul unghiului obtuz, este suficient pentru a găsi sinusul unghiului adiacent; pentru a găsi cosinusul, tangenta unui unghi obtuz, este necesar să se găsească numărul, opusul cosinusul, tangenta de colț adiacente.
De exemplu, păcatul 20 ianuarie ° = sin (1 80 ° - 120 °) = sin 60 ° =,
1 cos = 50 ° - cos (1 80 ° - 150 °) = - cos 30 ° = -,
tg 13 mai ° = - tg (1 80 ° - 135 °) = - tg 45 ° = - 1.
În cazul în care elevii de clasa au o pregătire matematică insuficientă, este posibil de a simplifica explicația. Este suficient să spunem că sinusul unui unghi obtuz este egal cu sinusul unghiului de cosinusul adiacent și și tangenta unui unghi obtuz este egal cu numărul de cosinus opus și tangenta unui colț adiacent.
Sinus 0 ° este 0, sinusul 180 ° este 0, sinusul de 90 de grade este egal cu 1, iar cosinusul 0 ° este egal cu 1, cosinus este -1 180 °, cosinus de 90 de grade este 0; Apoi tangente 0 ° și 180 ° sunt 0, iar tangenta 90 ° există.
IV. Consolidarea și înțelegerea materialului nou
1. Se calculează sinus, cosinus și tangenta unui unghi:
a) 120 °; b) 135 °; c) 150 °.
2. Cu ajutorul unui calculator (tabele), găsiți:
a) sin 100 °, 132 ° păcat, păcat 175 °;
b) cos 95 °, 127 ° cos, cos l 70 °;
a) tg 93 °, tg 129 °, 172 ° tg.
V. Tema
1. Pentru a studia definiția sinus, cosinus, tangenta unghiuri de la 0 ° la 180 °.
2. Cu ajutorul unui calculator (tabele), se calculează:
a) sin 105 °, 140 ° păcat, păcat 165 °;
b) cos 100 °, 130 ° cos, cos 160 °;
a) tg 103 °, tg 131 °, 163 ° tg.
VI. Rezumând rezultatele lecției
1. Definirea sinus, cosinus, tangenta unghiuri de la 0 ° la 180 °.
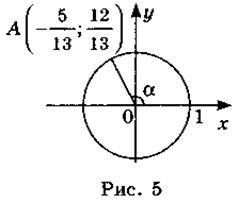
2. Consultați Fig. 5, găsit:
a) sin α; b) cos α; a) tg α.