Teorema privind proporționalitatea segmentelor care se intersectează și tangenta
(Tangenta proprietate și secanta efectuate de la un punct)
Pentru tangentă și secant unui cerc realizat dintr-un punct, distanța pătratică a acestui punct din punct de atingere egală cu produsul din lungimea sa o secant la lungimea porțiunii exterioare.
Cu alte cuvinte, pătratul distanței de la acest punct la punctul de contact este egală cu produsul dintre distanțele de la acest punct la punctele de intersecție ale unei secantă cu un cerc.
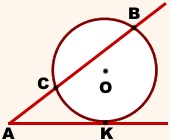
Având în vedere. env. (O; R), AK - tangent, AB - secantă
env. (O; R) ∩AK = K, (O; R) ∩AB = B, C
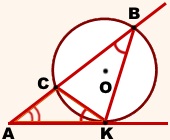
Luați în considerare ABK triunghiuri și AKC.
Ei ∠A - totală.
(Ca inclus unghi. CK bazat pe un arc).
triunghiuri De aici ABK și AKC similare (două colțuri).
Din similitudinea triunghiuri ar trebui să fie proporționale cu părțile lor respective:
Conform proprietății de bază al proporției
QED.
Un cerc cu centrul său pe latura triunghiului ABC AC trece prin vertex C și este tangent la linia AB la punctul B. Find AC, dacă diametrul cercului este egal cu 15, și AB = 4.
ΔABC, B, C ∈ env. (O; R) O∈AC, AB - tangent, AB = 4, FC - FC diametru = 15
Prin tangentă proprietate și secanta efectuate de la un punct,
Să AF = x, apoi AC = x + 15. Compoziția și rezolva ecuația:
A doua rădăcină nu este adecvată în sensul problemei. În consecință, AC = 1 + 15 = 16.