Exemplul 1 este necesar pentru a forma un vector x. format din 6 elemente. Elementele acestui vector este atribuit valorile indicelui.
Decizie. Noi oferim două opțiuni pentru a rezolva această problemă:
1. Utilizați variabila indexată;
2. Utilizarea komandyInserts-Matrix.
Pentru a forma un vector, utilizați variabila auxiliară, care va juca rolul unui index (de exemplu, i), iar apoi vom folosi această variabilă la valorile elementelor de construcție ale vectorului. Formarea vectorului este prezentată în Fig. 1.
Formarea x va produce folosind comanda Matrix. Pentru a face acest lucru, mai întâi scrie declarația de atribuire: „x =“, apoi urmați komanduMatrix. Această comandă deschide «Insert Matrix» caseta de dialog, care este prezentat în Fig. 2, care necesită un număr de rânduri și numărul de coloane. În acest exemplu, numărul de linii este egal cu 6, iar numărul de coloane este egal cu 1.

Fig. 1. Formarea vectorului utilizând variabila indexată
După apăsarea butonului «OK» Echipa va oferi un șablon cu șase celule, în care să intre valorile elementelor vectoriale.
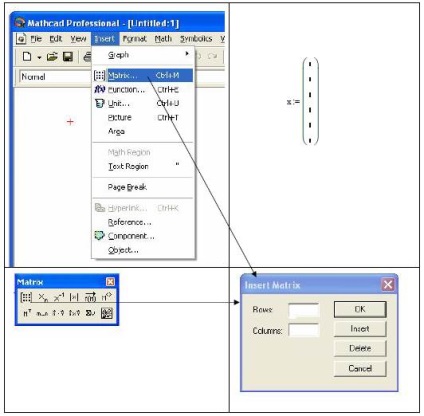
Fig. 2. Apel «Insert Matrix» pentru a crea o matrice folosind «Matrix» comanda de dialog
Exemplul 2. Într-un fișier denumit «int (4_4) .txt» număr sunt înregistrate într-o matrice de patru linii de patru elemente separate prin spații. Într-un fișier numit «int (4_1) .txt» a înregistrat numărul într-o coloană. Vrei să citiți datele din Q matrice și vectorul P.
Decizie. Pentru a citi date dintr-un fișier într-o matrice / vector puteți utiliza READPRN, care are un parametru - numele fișierului. Un fragment dintr-o soluție este prezentată în Fig. 3.
Fig. 3. Citirea datelor din fișiere
Cu matrici pot fi realizate atât calcule numerice și simbolice. Matrix Operațiuni în sistemul de MathCad notat așa cum se obișnuiește în matematică: -, +, *.
Fig. 4 prezintă atribuirea unor echipe specializate situate pe panoul instrumentovMatrix.
În plus, sistemul MathCAD este un număr mare de funcții pentru lucrul cu vectori si matrici. Pentru a utiliza aceste funcții pot utiliza funcția expertului f (x).

Fig. 4. Numirea unor echipe, situate în «Matrix» bara de instrumente
Fig. 5 prezintă calcule prin operații de matrice.

Fig. 5. Exemple de calcule ale matricei în MathCAD
Exemplul 3 necesar pentru a forma o matrice pătrată cu diagonala (6x 6). Valorile principalelor elemente diagonale trebuie să coincidă cu numărul rând / coloană.
Decizie. Pentru o matrice diagonală a sistemului asigură funcția diag. care are un parametru - vectorul elementelor diagonale. Prin urmare, formarea matricei incepe prin crearea unui vector auxiliar, în care elementele sunt aduse la o diagonală. Pentru formarea vectorului auxiliar (de exemplu, denumit s), folosim variabila auxiliară care va acționa ca un index (de exemplu, i). Apoi, formarea matricei diagonale poate fi obținută ca urmare a operațiilor, așa cum se arată în Fig. 6.
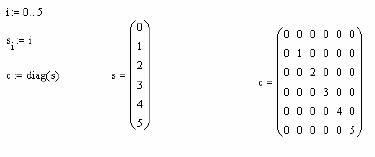
Fig. 6. Formarea unei matrice diagonală
Exemplul 4. Având în vedere cele două matrici: A (4x3) și B (4x 2). Necesită combina aceste matrice într-o singură matrice C (4x 5), în care, prima coloană a noii matrice trebuie sa fie coloane matricei A și la dreapta acestor elemente urmează coloanele matricei B (metoda „append dreapta“).
Decizie. Pentru a conecta două matrici într-o singură matrice poate fi utilizată funcția de augmentare. ce parametri vor fi numele matrice conectate, așa cum se arată în Fig. 7.

Fig. 7. Asociația a două matrice în conformitate cu regula „drept adăugarea“
Exemplul 5 Având în vedere două matrici: A (2x3) și B (3x3). Necesită combina aceste matrice într-o singură matrice C (5x3), în care, în noua matrice ca primul rând trebuie să fie rândurile A și pentru ei să urmeze rândurile B.
Decizie. Pentru a conecta două matrice într-o singură matrice conform regulii „sub reciproc“ funcție stivă poate fi folosită. ce parametri vor fi numele matrice conectate, așa cum se arată în Fig. 8.
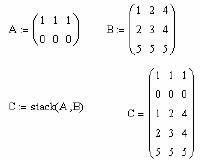
Fig. 8. Asociația a două matrice în conformitate cu regula „sub reciproc“
Exemplul 6. matricea A Dana (6x 6). Vrei să ieși din această matrice sub-matrice, care include elemente aranjate în rânduri, pornind de la numărul 2 la numărul patrulea, și coloane, începând cu numărul 0-lea la numărul cincea.
Decizie. Pentru a selecta o submatrice cu numere de rânduri și coloane reprezentate de valorile limită prevăzute funcția submatricii. Această funcție are cinci parametri: numele matricei de la care se face alegerea; alegerea inițială a numărului rând; numărul final linie de selecție; pornind de selecție coloană număr; alegerea finală a numărului coloanei. O posibilă soluție este prezentată în Fig. 9.

Fig. 9. Izolarea submatricile date matrice
Exemplul 7 este dată matricea A (6x6). Vrei să ieși din această matrice doi vectori. Primul vector trebuie să coincidă cu a patra coloană a matricei A, iar al doilea - din al treilea rând al matricei A.
Decizie. Pentru vector de valori pe care le puteți utiliza comanda M <> (Ia din vectorul coloană de matrice), care este dispus pe «Matrix» panou. Pentru primul vector această comandă trebuie să fie aplicat direct matricei A, iar pentru al doilea vector trebuie să fie mai întâi obținut din matricea transpusa matricei A, și numai apoi utilizați comanda „ia coloana.“ O posibilă soluție este prezentată în Fig. 10.
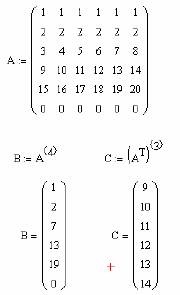
Fig. 10. Izolarea valorilor vectoriale din matricea predeterminată
Exemplul 8. Din matricea A (6x 6) alocă Minor, care este format prin ștergerea din această matrice linia zero și a treia coloană.
Decizie. Soluția de rezolvare a problemei poate fi redusă la un compus din doi submatricile extrase din matricea A, așa cum se arată în Fig. 11.
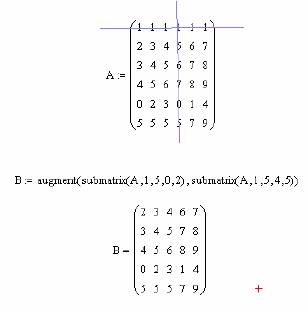
Fig. 11. Izolarea matrice dată minor
Folosind matrice pentru
efectuarea operațiunilor de matrice în sistemul MathCAD
Este cunoscut faptul că, ca rezultat al matrice de multiplicare printr-un vector obținut prin vectorul. Mai mult decât atât, fiecare element al th j- rezultatului vectorului reprezintă suma produselor elementelor pereche ale corespunzătoare ale rândului i -lea al matricei la elementele vectorului-factor. Evident că, în cazul în care vectorul, care este multiplicat cu matricea, toate elementele sunt egale cu zero și un element este egal cu unu, rezultatul unui astfel de produs va fi numărul corespunzător acelui element j- rând lea al matricei în care un factor este un vector unitate. O astfel de concluzie poate fi utilizată pentru selecția (formarea) a coloanei dorite a matricei.
Exemplul 9. Dana matrice: A (4x4). Vrei să ieși din această matrice doi vectori. Primul vector trebuie să se potrivească cu coloana 0th a matricei A, iar al doilea - cu a treia coloană a matricei A.
Decizie. Pentru noi vectori formează două vectorul auxiliar: vectorul B 1 - cu o singură valoare în rândul No. 0 și al doilea vector V 4 - cu o valoare unitară în numărul rândului 3. Apoi, pentru a obține vectori în conformitate cu starea problemei este suficientă pentru a se multiplica O matrice din dreapta vectorilor B 1 și B 2 după cum se pare în Fig. 12.
Fig. 12. Izolarea valorilor vectoriale din matricea predeterminată
In mod similar, se poate obține vectorul rând al matricei. Este suficient pentru a forma un vector auxiliar rând, în care toate componentele sunt egale cu zero, iar componenta una, număr care corespunde eliberat din rândul de matrice este egal cu unitatea. Dacă acest vector este multiplicat pe stânga de matrice, rândul dorit este obținut ca rezultat.
Exemplul 10 Dana matrice: A (4x 4). Necesita izolat din primul rând al matricei în ordine (cu indexul 0).
Decizie. În primul rând, se prepară vectorul rând auxiliar necesar și apoi se înmulțește această linie lăsate de matricea A. Linia vector poate fi obținut din Exemplul transpusa anterioară a coloanei vectorului B 1.
Această metodă poate fi folosită pentru permutarea de rânduri și coloane ale matricei, dar acest lucru va necesita mai susținere matrice formată din vectori coloană (vectori rând), plasați elemente individuale care corespund ordinului care trebuie să fie păstrate în matricea de transformare.
Exemplul 11 Dana matrice: A (4x 4). Necesita rearanjat într-o matrice cu rânduri numerotate 0 și 1.
Decizie. Pentru a converti matricea originală este necesară pentru a pregăti o matrice de susținere. În locația auxiliară matrice rânduri în unitățile trebuie să corespundă cu ordinea dorită pentru a poziționa un nou rând în matrice. După aceea, soluția poate fi obținută prin multiplicarea matrici:
Exemplul 12 Dana matrice: A (4x4). Necesita rearanjat într-o matrice cu coloane numerotate de la 0 și 1.
Decizie. Pentru a converti matricea originală este necesară pentru a pregăti o matrice de susținere. În unitățile auxiliare din locația coloanele matricei corespund ordinea dorită pentru a le selecta într-o matrice nouă. După aceea, soluția poate fi obținută prin multiplicarea matrici:
Astfel, prin utilizarea vectorului auxiliar cu componente individuale primi vector ale cărui componente sunt egale cu suma linii (coloane) matrice, și cantitatea de coloane selectate separat (linii).
Exemplul 13 Dana matrice: A (4x4). Necesar pentru a găsi suma elementelor din coloana cu numărul 3.
Decizie. Pentru a rezolva problema pe care doriți să pregătească un vector rând auxiliar al celulelor unitare și pentru a se multiplica:
Exemplul 14 Dana matrice: A (4x4). Necesară pentru a obține un vector ale cărui elemente vor fi reprezentate de suma elementelor din coloanele matricei.
Decizie. Pentru a prepara soluții necesită vector rând auxiliar de celule unitate și de a efectua multiplicarea:
1. Cum se determină variabila indexate?
2. Ce tipuri de matrice în MathCAD știi?
3. Care variabile de sistem definește limita inferioară a elementelor de indexare matrice?
4. Descrie modul de a crea matrice în MathCAD.
Funcții 6. Bara de instrumente care conține lucra cu matrici în MathCAD.
7. Lista posibil pachet MathCad atunci când se utilizează o matrice.
8. Cum pot obține un vector rând al matricei?
9. Care sunt funcțiile utilizate în alocarea minorului a matricei?
10. Care sunt functiile folosite in matrici de asociere?
Variante de sarcini la numărul de lucru de laborator 2
Expresia Sarcina 1. Se calculează în conformitate cu un exemplu de realizare. Una dintre matricile introduse folosind fișier .txt.
Ținta 2. matrice Conversia în conformitate cu varianta de realizare de referință. Valorile matrici arbitrare.
Opțiunea 1: Din matricea A (5x5) alocă Minor, care este format prin ștergerea din această linie patra matrice și coloana 0th.
Opțiunea 2: Dana matrice: A (6x4). Necesita izolată din a doua matrice a liniei de comandă (numerotate de la 1).
Opțiunea 3: Dana matrice: A (4x4) și B (5x5). Necesar din aceste matrici sunt doi vectori. Primul vector trebuie să coincidă cu a patra coloană a matricei A și a doua - coloana 0-lea al matricei B.
Variantei 4. Deoarece matricea A (4x4) alocă Minor, care este format prin eliminarea din a doua linie a matricei și a doua coloană.
Întruchipare 5. Necesită forma diagonală pătrat matrice C (5x5). Valorile principalelor elemente diagonale trebuie să coincidă cu numărul rând / coloană.
Întruchipare 6. Dana matrice: A (3x3). Vrei să ieși din această matrice doi vectori. Primul vector trebuie să se potrivească cu coloana 0th a matricei A, iar al doilea - cu a treia coloană a matricei A.
Întruchipare 7. Având în vedere două matrici: A (2x2) și B (4x2). Necesită combina aceste matrice într-o matrice singură C (6x2), în care, în noua matrice ca primul rând al matricei B trebuie să fie un șir de caractere, dar pentru ei să urmeze rândurile de A.
Întruchipare 8. Având în vedere două matrici: A (4x3) și B (4x2). Necesită fir unirea acestor matrice într-o matrice singură C (4x5), și, prima coloană a noii matrice trebuie să fie coloanele matricei A și dreptul acestor elemente-polițiștii urmează coloanele matricei B (prin „adăugarea la dreapta“).
Opțiunea 9 este necesară pentru a forma o matrice pătrată diagonală (6x6). Valorile principalelor elemente diagonale trebuie să coincidă cu numărul rând / coloană.
Întruchipare 10. Date fiind matricea: A (4x5) și B (4x2). Necesita izolat din primul rând al matricei A în ordine (numărul 0) și pentru a combina șirul rezultat cu matricea B (metoda „append dreapta“)
Sarcina 3. Rezolvarea sistemului de ecuații liniare (Slough) de Cramer.