Semne ale unui paralelogram (slide-7)
Proprietatea - sunt un semn al conversa.
1) În cazul în care perechea de patrulater laturile opuse sunt paralele și egale, atunci patrulaterul - un paralelogram.
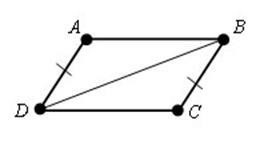
AD = BC, AD || BC, ABCD - paralelogram
2) În cazul în care diagonalele Intersect patrulater și punctul de intersecție sunt împărțite în jumătate, atunci acest patrulater - un paralelogram.
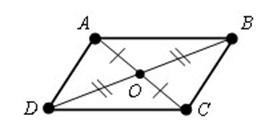
AB = OC
BO = OD, ABCD - paralelogram
3) Dacă patrulatere opuse unghiurile sunt egale, un dreptunghi - un paralelogram.
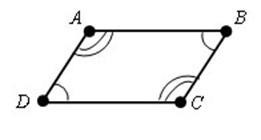
A = C
B = D, atunci ABCD - paralelogram
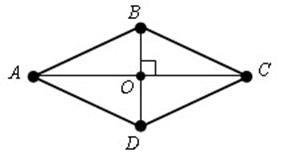
Definiție: Este un paralelogram care are toate laturile egale.
1) returna toate proprietățile unui paralelogram
2) diagonalele rombului se intersectează în unghiuri drepte. Diagonalele unui romb sunt Bisectoarele unghiurilor
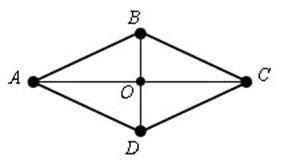
ABCD - un diamant, atunci; AC, DB - Bisectoarele unghiurilor
În cazul în care diagonalele unui paralelogram sunt perpendiculare, atunci paralelogramului - un diamant.
3. dreptunghi (slide 8-10)
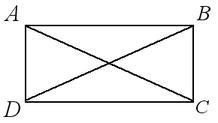
Definiție: dreptunghi este numit un paralelogram în care toate unghiurile sunt unghiuri drepte.
1) returna toate proprietățile unui paralelogram
2) diagonalele AVSDpryamougolnik ale dreptunghiului sunt apoi AC = BD.
Un semn al dreptunghiului: În cazul în care paralelogram diagonalele sunt egale, atunci este un dreptunghi.
ABCD - un paralelogram; AC = BD ABCD - dreptunghi
Definiție: Pătratul - un paralelogram în care toate unghiurile sunt unghiuri drepte și laturile sunt egale; dreptunghi în cazul în care toate părțile sunt egale; diamant, în cazul în colțuri - drepte.
1) Proprietățile paralelogramului
2) Proprietățile dreptunghiului
3) romburi Proprietăți
5. Trapezoid (culisa 15-17)
Definiție: Trapezoid - un patrulater în care cele două părți sunt paralele, iar cele două părți nu sunt paralele. laturile paralele sunt numite baze ale trapezoid, Celelalte două (BC și AD.) - părțile laterale (AB și CD).
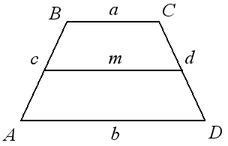
trapez isoscel, ale cărui laturi sunt egale cu AB = CD
1) Unghiurile de bază sunt egale cu:
2) Diagonalele sunt: CA = DB
Simptom: Dacă unghiurile trapezoidală de la baza sunt egale, atunci este isoscel. Dreptunghiular - un trapez în care un unghi este de 90 °.
III. Sarcini (diapozitiv 18-43)
1. Într-un ABCD paralelogram. Unghiul A este de 30 °. Găsiți unghiurile unui paralelogram.
2. Perimetrul paralelogramului este egală cu 200 cm. Una dintre laturile este de 25 cm. Găsiți laturile rămase ale paralelogramului.
3. Partea AB paralelogram ABCD este de 10 cm. Diagonalele AC și BD se intersectează într-un punct. O și sunt egale cu 14 cm și 10 cm. Gasiti perimetrul triunghiului AOB.
4. Probleme cu alegerea răspunsului
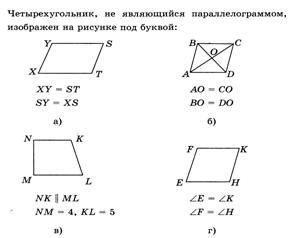
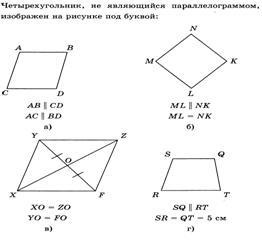

5. În patrulater ABCD BC = AD și AD || Sun, BAC + ACD = 80 o. Găsiți ceea ce este fiecare dintre aceste unghiuri.
6. În ABCD patrulater BA = CD și AB || DC, CBD = 15 o. Care este unghiul de VDA?
7. paralelogram KMNP transportate bisector direcție MKP, MN care se intersectează în punctul E. Găsiți partea paralelogram KR KMNP dacă UI = 8 cm, iar perimetrul paralelogramului este de 40 cm.
1. Perimetrul dreptunghiului este de 28 cm, iar una din laturile sale, cel puțin un alt 4cm. Apoi, partea mai mică este egală cu?
2. Într-un colț al dreptunghiului format de diagonalele egal cu 120 °. Partea cea mai mica a dreptunghiului este de 8 cm. Gaseste diagonala dreptunghiului.
3. ABCD dreptunghi persekayutsya în diagonală la O. ACD = 60 o. BD = 10 cm. Găsiți partea CD.
4. dreptunghiului ABCD diagonală sunt oprite la punctul O. BAC = 50 o. Punctul E - mijlocul AB. Găsiți unghiul de EOD.
5. Problema cu alegerea răspunsului:

1. Probleme cu alegerea răspunsului:
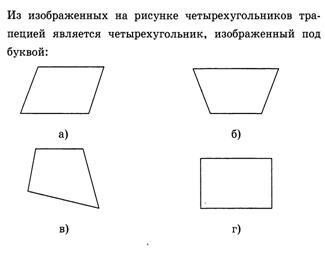



2. trapezoidală MNKL diagonal MK KL, NMK = KML = 30 °. Perimetrul trapezului este egală cu 30 cm. Find NK.
3. dreptunghiular trapezoidală unghi ascuțit este de 45 °. Mai mici latura și baza mică egală cu 10 cm. Găsiți baza mai mare.
1. diamant Unghiul ABCD este egal cu 31 °. Diagonalele se intersectează în punctul O. Găsiți unghiurile triunghiului BOC.
2. romburi ABCD Despre - punctul de intersecție al diagonalelor, E și F sunt punctele mediane ale BC și DC. Demonstrati ca EF = BO EF și AC.
3. romburi ABCD Despre - punctul de intersecție al diagonalelor, OM, OK, OE - perpendicularele a scăzut la laturile AB, BC, respectiv CD-uri. Demonstrati ca OM = OK. Găsiți suma unghiurilor Memorandumul de înțelegere și CDE.
4. Găsiți unghiuri diez dacă unul dintre unghiurile este de 70 °.
5. ABCD romburi cu latura de 5 cm, unghiul AVD este de 60 ° și perimetrul diagonal Analizate BD.
1. În figura ABCD - un dreptunghi. Demonstrati ca patrulaterul este un pătrat al CIPD.
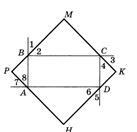
2. În triunghiul ABC B = 90 o. AB = BC. Pe AB lateral și BC luat punctele M și R. In partea AC - punctele K și H, astfel încât mARN patrulater - este un pătrat. MR = un cm. Gaseste AC.
3. Figura patrulater ABCD - pătrat. AK = PD = EC = BM. Demonstrati ca MERCK - un pătrat.
1. clasele Textbook Geometrie 7-9, ed. Atanasyan LS
2. Ziv BG „Geometrie Materiale didactice“ Grad 8
3. Workbook privind geometria Atanasyan LS
4. AV Farkov „Teste de geometrie“ Grad 8