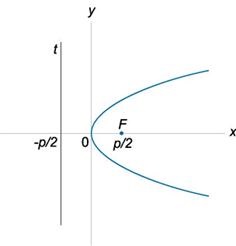
O parabolă este o curbă plană fiecare punct pe care următoarea proprietate: distanța până la un punct predeterminat (focalizare parabolei) este distanța până la o linie predeterminată (directricea parabolei). Distanța de la focalizarea la directricea parabolei, și a numit parametrul este notat cu p. Un parabole are o singură axă de simetrie care se intersectează parabolei în partea sa superioară. ecuația parabolei Canonical are forma: y = 2px.
ecuația directricea: x = -p / 2,
unde p - parametrul parabolei.
Excentricitatea: focus Coordonate: F (p / 2, 0) vertex coordonatele M (0, 0)
Ecuația generală a Ax parabolei 2 + Bxy + Cy 2 + Dx + Ey + F = 0, unde B 2 - 4AC = 0.
Ecuația parabolei, axa de simetrie care este paralelă cu axa Oy: Ax 2 + Dx + Ey + F = 0 (A ≠ 0, E ≠ 0)
sau într-o formă echivalentă: y = ax 2 + bx + c, p = 1 / (2a)
Directricea Ecuația: y = y0 - p / 2, unde p - parametru al parabolei.
Coordonatele focus: F (x0 y0 + p / 2).

y = ax 2 p = 1 / (2a)
Directricea ecuația y = -p / 2, unde p - parametru al parabolei.
Coordonatele focus: F (0, p / 2) al nodului coordonatelor: M (0, 0)