Este dificil să se supraestimeze importanța problemelor de programare liniară pentru economia de astăzi și industrie. Cu toate acestea, metoda grafică, deși are simplitatea, nu pot fi utilizate în aplicații din cauza limitărilor sale. Prin urmare, metoda simplex a devenit popular. care să permită rezolvarea problemelor de orice complexitate și dimensiune.
Vă mulțumim pentru lectură și pentru partajarea cu alții
Originile metodei simplex și esența ei
Metoda simplex pentru rezolvarea problemelor de programare lineară a fost dezvoltat de matematicianul american George Dantzig. De asemenea, o mare contribuție la dezvoltarea sa a fost făcută de către oamenii de știință Kuhn și Tucker, mai bine cunoscut pentru evoluțiile sale în domeniul programării neliniare.
Esența metodei simplex este următoarea: pentru a maximiza (sau a minimiza) un criteriu în constrângerile liniare suprapuse. Acest criteriu poate fi un venit brut din vânzarea produselor, cheltuielile totale de exploatare pentru producția de bunuri și așa mai departe.
La aceleași variabile care afectează valoarea criteriului, suprapusă constrângerile liniare sub formă de ecuații sau inegalități. În esență, metoda simplex - un sistem avansat probleme grafice metodresheniya LP într-un spațiu multidimensional.
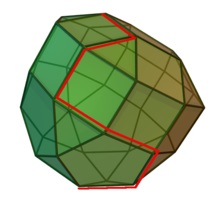
La fel ca și o metodă grafică de a căuta optime în nodurile poligonale în metoda simplex, optimul este solicitată la nodurile poliedru n-dimensional, numit simplex (a se vedea schematic în Figura simplex ;. Red arată calea de la punctul de referință la punctul optim).
Algoritmul metodei simplex
Procedura poate fi rezumată după cum urmează:
- sistem de restricție prin transformare conduce la necesitatea, așa-numita bază, sub formă;
- este așa-numita soluție de referință care servește „punct de plecare“;
- iterează prin nodurile. Dacă în acest moment mai mult decât valoarea criteriului (sau mai mic), cel anterior, atunci procesul continuă. Când valoarea criteriu nu poate fi îmbunătățită, apoi se găsește o soluție.
Adică, sensul metodei simplex este următoarea: toate inegalitățile liniare, care în spațiul multi-dimensional corespund semiplanul, limita un simplex. În acest caz, ecuația care descrie criteriul optimizat corespunde hiperplan. Acum, trebuie doar pentru a găsi în partea de sus a simplex, ambele aparținând hiperplanul, coordonatele care maximizează (minimizarea) criteriul. Prin urmare, baza selectată și vârful ei ne deplasăm de la un nod la altul, până când vom găsi punctul optim.
Un exemplu practic al aplicării unei metode simplex
Metoda Simplex va rezolva problema. Maximizarea funcția $$ L = X + Z \ rightarrow \ max $$ sub constrângeri $$ \ left \<\begin Y-X+Z=1,\\ X-2Z+T=2. \end \right. $$ У нас есть четыре переменные – $X, Y, Z, T$ – причем критерий зависит лишь от двух переменных. Примем $Т$ и $Y$ за базисные переменные и выразим их через остальные две свободные переменные. Получим:
Când $ X $ și $ Z $ este egala cu zero, variabilele de bază sunt $ Y = 1, T = 2 $. Valoarea Criteriu $ L = 0 $. Deci, punctul $ (1,0,0,2) $ este o soluție bazică. Să începem sortarea nodurile. Mărește criteriu poate fi mărit $ Z $ la unitate. Apoi, la $ Z = 1, X = 0 $ variabile de bază ia valori $ Y = 0, T = 4 $. Noua soluție fezabilă - un punct $ (0,0,1,4) criteriul $ este $ L = 1 $.
Acum ne-am exprima $ Z $ și $ T $ de $ Y $ si $ X $:
Mărește $ L $ poate fi crescut doar $ X $. Cu toate acestea, $ X $ poate fi crescută pe termen nelimitat, sistemul original de ecuații. În consecință, criteriul $ L $ va avea valori infinit mari, rezolvarea problemei prin metoda simplex nu există. În acest caz, se spune că un caz de simplex infinit.
Alte exemple de rezolvare a problemelor de programare liniară pot fi găsite în secțiunea: (! Zece exemple) probleme de programare liniară cu soluții.
Vă mulțumim pentru lectură și pentru partajarea cu alții