Noi explicăm conceptele de bază asociate cu utilizarea metodelor numerice.
Vom introduce grila variabilă t uniformă cu pasul h> 0. și anume ia în considerare setul de puncte.
1. Metoda lui Euler. Ecuația (3.1) se înlocuiește cu ecuația diferența
.
Soluția acestei ecuații este în mod clar pe formula recurenta.
Metoda de eroare. În cazul în care

La capitolul 6 am studiat:
problema Cauchy pentru o primă ecuație diferențială.
Metodele pentru soluția numerică a ecuației diferențiale de prim ordin.
Metoda lui Euler și eroarea.
Runge-Kutta precizie a doua ordine și eroare.
Metoda Runge-Kutta al treilea ordin de precizie și de eroare.
Metoda Runge-Kutta a patra precizie ordine și eroare.
2. Metoda Runge - Kutta precizie de ordinul doi.
Să presupunem că o valoare aproximativă



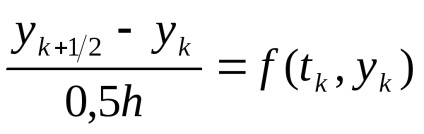
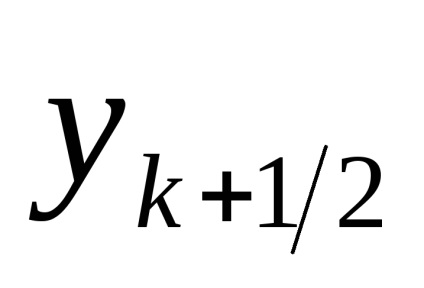

Metoda de eroare. În cazul în care

3. Metoda de Runge - Kutta precizie pentru a treia.
Noi credem că soluția problemei (3.1) - (3.2) la punctul

, unde

4. Runge - Kutta precizie a patra comandă.

, unde

Notă. Metoda Runge-Kutta se aplică și în cazul în care funcția necunoscută este un vector, adică,
Prelegerea 7 am învățat:
Runge-Kutta precizie a doua ordine și eroare.
Metoda Runge-Kutta al treilea ordin de precizie și de eroare.
Metoda Runge-Kutta a patra precizie ordine și eroare.
Finite-diferență de aproximare a primei derivate și precizia acesteia.
Finite-diferență de aproximare a derivatei a doua și acuratețea acestuia.
Aproximarea finita diferență a primei derivate și derivata a doua se obține din determinare. Folosind extinderea funcțiilor într-o vecinătate a lui x în seria Taylor cu restul sub forma lui Peano, avem dreptul și diferențele finite la stânga, precum și o aproximare a derivatei a doua.
Prelegerea 8 am învățat să aproximeze prima și a doua derivate ale funcției.
Problema transferului de căldură în conducta de transport de petrol.
Un model matematic al problemelor de transfer de căldură în conducta de transport de petrol.
§ 4. Problema transferului de căldură în conducta de transport de petrol. Ecuațiile diferențiale de ordinul al doilea. problemă valoarea limită
Primul tip.
4.1. Declarația problemei.
Sarcina 4. conductă lungă cu o conductivitate termică X (kcal / m.chas deg.) Este în echilibru termic, adică, puncte de conducte nu se schimbă temperatura cu timpul. Pierderea de căldură prin suprafața țevii în mediu a cărui temperatură θ0 = const. este proporțională cu diferența de temperatură cu un coeficient de transfer termic α constant (kcal / m2 h ° C.). Presupunând temperatură θ în toate tochah secțiunea transversală a țevii constant, găsi dependența de θ = θ (x) pe coordonatele, măsurată de la orice capăt.