Definiție: fracții elementare numite următoarele patru tipuri:
m, n - întregi (m ³ 2, n ³ 2) și b 2 - 4ac <0.
Primele două tipuri de integralelor de fracții elementare sunt destul de simplu de masă înlocuind t = ax + b.
Să considerăm o metodă de integrare a fracțiunilor elementare ale formei III.
fracțiune de tip integral III poate fi exprimată ca:
Este prezentată într-o formă generală turnate tip integral fracțiunile III la două integralele tabelare.
Luați în considerare aplicarea formulei de mai sus în exemple.
In general vorbind, în cazul în care expresia + trinomial ax 2 bx + c b 2 - 4ac> 0, atunci fracția este prin definiție nu o unitate, dar cu toate acestea, este posibil să se integreze metoda de mai sus.
Considerăm acum metoda de integrare a parțiale de tip fracții IV.
În primul rând, considerăm cazul special cu M = 0, N 1 =.
Apoi tip integral poate fi realizată prin selectarea într-un numitor pătrat perfect reprezentat. Facem următoarea conversie:
A doua Integrala în această ecuație, vom lua fragmentar.
Pentru integrala originală obținem:
Formula rezultată se numește o recurență. Dacă aplica n-1 ori, obținem standardul integralei.
Ne întoarcem acum la integralei fracțiilor elementare de forma IV, în general.
În prima ecuație integrală obținută prin substituirea
2 + s este dat în tabel. o formulă de recurență aplică discutat mai sus pentru a doua integrală.
În ciuda complexității aparente a fracțiunilor elementare de tip integrare IV, în practică, este destul de ușor de utilizat pentru fracțiuni cu un grad mic n. și universalitatea și generalitatea abordare face posibila o implementare foarte simplă a acestei metode pe un computer.
Pentru a integra fracția rațională este necesară pentru a se descompune în fracții elementare.
Teorema: Dacă - fracțiune rațională adecvată, numitorul P (x) este reprezentat ca un produs al factorilor liniare și pătratice (rețineți că orice polinom cu coeficienți reali pot fi prezentate sub forma: P (x) = (x - a) ... (x - b) b (x 2 + px + q) l ... (x 2 + rx + s) m), atunci această fracție poate fi descompusă în elementar conform următoarei scheme:
În integrarea fracțiilor raționale a recurge la descompunerea inițială în fracții elementare. Pentru a găsi valorile din Ai. Bi. Mi. Ni. Ri. Si se utilizează așa-numita metodă de coeficienți nedeterminate. esența care constă în faptul că, pentru două polinoame sunt identic egale, este necesar și suficient să fie egală cu coeficienții de puteri, cum ar fi de x.
Aplicarea acestei metode considerăm un exemplu specific.
Ceea ce duce la un numitor comun și echivalarea numărătorilor corespunzătoare, obținem:
pentru că împușcat greșit, acesta trebuie să fie mai întâi izolate din întreaga parte din ea:
Descompunem numitorul fracțiilor obținute factorizării. Se observă că, atunci când x = 3, numitorul devine zero. apoi:
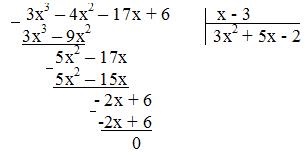
Astfel 3x 3 - 4x 2 - 17x + 6 = (x - 3) (3x 2 + 5x - 2) = (x - 3) (x + 2) (3x - 1). apoi:
Pentru a evita nedeterminat în cazul suporturilor dezvălui coeficienți, gruparea și soluții ale sistemului (care poate fi destul de mare, în unele cazuri), se utilizează o metodă numită valori arbitrare. Metoda constă în faptul că expresia derivată de mai sus substituită alternativ mai multe (în funcție de numărul de coeficienți nedeterminat) valori arbitrare ale lui x. Pentru a simplifica calculele luate ca valori arbitrare luând punctul în care numitorul fracției este zero, adică în cazul nostru - 3, -2, 1/3. obținem: