
Acasă | Despre noi | feedback-ul
Una dintre aplicațiile derivate - regula L'Hospital în calcularea limitelor (în caz de incertitudini și):
2.31. Găsiți limitele regula L'Hospital lui:
studiu funcție în monotonie,
Extremele și umflatura.
Asimptotă graficului
Opredelenie.Kriticheskoy funcție punct y = f (x) este un punct în care derivatul este egal cu zero sau nu există.
Teorema. Dacă intervalul (a, b) derivatul este pozitiv / negativ, atunci intervalul funcției crește / descrește.
Teorema. Dacă trec prin punctul critic al modificărilor derivate semn de la „+“ la „-“ (cu „-“ la „+“), apoi - punctul funcției maxime (minime)
Definiția. Funcția Convex este numită în sus (în jos) în intervalul (a, b), în cazul în care punctul în acest interval sunt generate în cadrul (de mai sus) tangentele construite la aceste puncte. Punctul de inflexiune al graficului este numit un punct care se împarte în secțiuni cu direcții diferite de convexitate.
Exploreaza funcția în monotonia și extreme, convexitate.
1. studiază funcția pe monotonia și extreme.
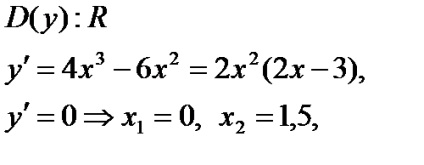
Fa un desen (fig. 2.1).
Se calculează ordonatele punctelor de inflexiune a graficului:
Coordonatele punctelor de inflexiune: (0, 0), (1, -1).
2.32. Exploreaza funcția în monotonia și extreme:
2.33. Găsiți cel mai mic și cel mai mare znacheniyafunktsii:
1) în intervalul [2; 4];
2) în intervalul [-1; 1];
3) în intervalul [-4; 4];
4) în intervalul [-2; 1].
2.34. Costurile de producție C (y .. e) sunt dependente de cantitatea de ieșire x (u): Găsiți cele mai mari costuri de producție, în cazul în care x variază în intervalul [2; 7]. Găsiți valoarea lui x. în care profitul este maximizată în cazul în care veniturile din vânzarea unei unități de producție este egală cu 15. e.
2.35. Doriți să selectați o suprafață de teren dreptunghiular de 512 m 2 la gard și împărțit printr-un gard în trei părți egale în paralel cu o parte a platformei. Care ar trebui să fie de mărimea zonei pentru paza a mers pe cea mai mică cantitate de material?
2.36. Pentru un anumit perimetru dintr-o cutie dreptunghiulară găsit dimensiunile sale, astfel încât acesta lipsea cea mai mare cantitate de lumină.
2.37. Găsiți profitul maxim în cazul în care venitul din costurile R & C sunt determinate prin formulele: unde x - valoarea bunurilor vândute.
2.38. Dependența producției de ieșire W a costurilor de capital pentru funcția definită Găsiți intervalul de variație K pe care majorarea cheltuielilor de capital este ineficientă.
2.39. funcția de cost este venitul din vânzarea unei unități de ieșire este 200. Găsiți valoarea optimă pentru producția producătorului.
2.40. Dependența volumului producției (în termeni monetari) din costul capitalului este determinată de intervalul de valori ale funcției Find. care crește costul capitalului ineficient.
2.42. Veniturile din producția cu utilizarea unităților de resurse este o valoare resursă preț unitar - 10 den. u Ce cantitate de resurse ar trebui să fie achiziționate la profit a fost cea mai mare?
2.43. funcția de cost este venitul din vânzarea unei unități de producție este egal cu 50. Găsiți profitul maxim care se poate obține producătorul.
2.44. Dependența de monopol venit pe numărul de produse este definit ca funcția de cost de pe acest interval a forma Găsiți valoarea optimă pentru producția de monopol.
2.45. Prețul pentru producătorul de monopol de producție este stabilit în funcție de raportul identificat ca fiind. La ce valoare a eliberării de veniturile sale de vânzări va fi cea mai mare producție?
2,46. Funcția de cost are formularul de mai jos atunci când sub. În acest moment, nivelul de ieșire În ce condiții privind parametrul p companie profitabilă pentru a reduce producția, în cazul în care veniturile din vânzarea unei unități de producție este egal cu 50?
2.47. Găsiți un punct de inflexiune, și intervale de convexitate a graficului funcției:
2,48. Găsiți asimptota graficului:
Notă. Vertikalnayaasimptotaimeet ecuație x = a, în cazul în care cel puțin una dintre limitele funcției unilaterale x = a este egal cu ∞.
Naklonnayaasimptota are ecuația