Luați în considerare unele dintre sarcinile pe similaritatea triunghiuri.
I. În triunghiul ținut segment lateral paralel. punctele finale se află pe celelalte laturi ale triunghiului.
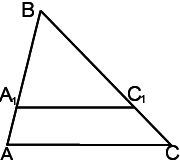
Luați în considerare triunghiuri ABC si A1BC1.
Rezolva problemele care implică triunghiuri similare convenabil folosind redare a culorilor, astfel încât vom selecta triunghiuri de date în culori diferite:
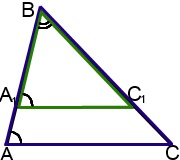
1) ∠ B - totală;
2) ∠ BAC = ∠ BA1C1 (ca și unghiurile respective de la AC ∥ A1C1 și secantă AB).
În consecință, ABC și A1BC1 triunghiuri sunt similare (două colțuri).
Din asemănarea triunghiurilor să fie proporțională cu laturile corespunzătoare:
O linie paralelă cu AC laterală a triunghiului ABC intersectează partea AB la punctul A1 și direcția soarelui - la punctul B1. Găsiți lungimea segmentului A1C1, în cazul în care AC = 35, AA1: A1B = 2: 5.
Demonstram similaritatea triunghiuri ABC și A1BC1.
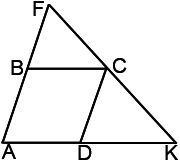
Luați în considerare triunghiul AFK și BFC.
Selectați datele din triunghiul de culoare.
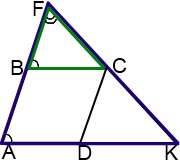
1) ∠ F - totală;
2) ∠ FAK = ∠ FBC (ca și unghiurile corespunzătoare cu AD ∥ BC și secantă AB).
În consecință, triunghiurile sunt similare AFK și BFC (două colțuri).
Din asemănarea triunghiurilor să fie proporțională cu laturile corespunzătoare:
Rombul inscripționată triunghi AFK ABCD, astfel încât unghiul A la care totalul din vertex C aparține parte FK. Găsiți direcția rombul, dacă AF = 21 cm, AK = 24 cm.
AFK dovedesc similitudinea triunghiuri și BFC. Dintre cele trei relații noi alegem cele pe care le știm ceva:
Noi luăm partea rombul pentru x:
Apoi, BF = AF-AB = 21 cm-x. Prin urmare,
Împărțind ambele părți de 3, obținem:
Data viitoare când ia în considerare problemele pe triunghiuri similare din trapez.