Numerele complexe au apărut în legătură cu sarcina de a rezolva ecuații pătratice. Stau în setul de numere reale, este imposibil de a rezolva o ecuație pătratică, care este discriminantul este mai mică decât zero.
Numerele complexe sunt utilizate în diferite aplicații ale matematicii. În special, teoria funcțiilor complexe este un instrument puternic în utilizarea metodelor matematice în diferite domenii ale științei.
Un număr complex este o expresie a formei în care sunt numere reale, unitatea imaginară.
Astfel, un număr complex este orice pereche ordonată de numere reale și a numerelor reale se numește abscisa unui număr complex număr real al ordonatei sale
Orice număr complex poate fi reprezentat pe un plan sub forma unui plan punct pe care sunt reprezentate de numere complexe, numit planul variabilei complexe
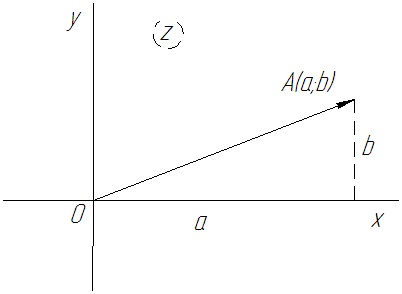
planul complex
Numerele reale sunt reprezentate de puncte abscisa numere imaginare sunt reprezentate prin puncte de coordonate. De aceea, axa se numește axa reală și, pe axa ordonatelor este axa imaginară.
Prin punctul de conectare la origine, obținem un vector în unele cazuri, este convenabil să ia în considerare imaginea vector geometric al unui număr complex În acest caz, părțile reale și imaginare ale vectorului sunt proiecțiile de pe axa reală și imaginară.
Notăm coordonatele polare și pol de numărare punct de origine și axa polară axa direcție pozitivă.
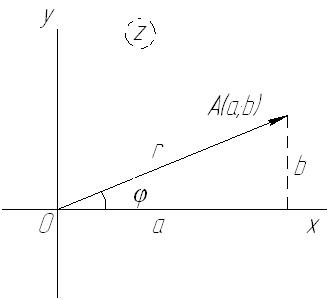
imagine geometrica a unui număr complex
Apoi egalitățile
Prin urmare, un număr complex poate fi reprezentat ca
- aceasta este forma trigonometrică a unui număr complex se numește modulul numărul argumentului complex al unui număr complex