Cel mai simplu este o linie dreaptă. Diferite moduri de stabilire meci direct într-un sistem dreptunghiular, diferite tipuri de ecuații sale coordonate.
Ecuația de o linie dreaptă cu pantă
P
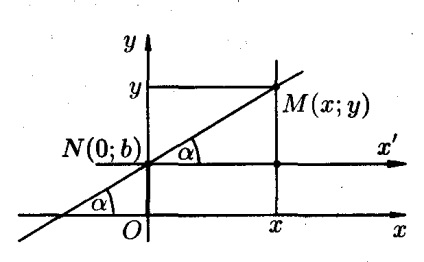
O pantă unghi α (0≤α≤π) a liniei se referă la cel mai mic unghi, ceea ce este necesar pentru a transforma în jurul punctului de intersecție al liniei și axa Ox antiorar până sale axa x coincide cu linia dreaptă.
Luați direct prin punctul M arbitrar (x, y) (vezi fig ..). Prin punctul Νh Ν „axa paralelă cu axa Ox și la fel îndreptate spre ea. Unghiul dintre axa Νh „și o linie dreaptă este α. Sistemul Νh'u punctul M are coordonatele x și (y - b). Din definiția de tangenta a egalității
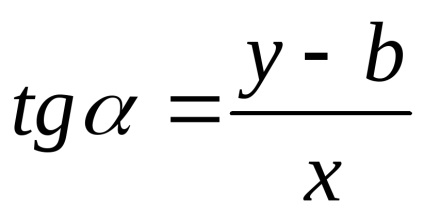
care satisfac coordonatele oricărui punct M (x, y) a liniei. Se poate observa că coordonatele oricărui punct P (x, y), situată în afara unei linii date, ecuația (10.2) nu sunt îndeplinite.
Numărul k = tg α numit linia pantei și ecuația (10.2) - ecuația liniei cu o pantă.
Dacă linia trece prin origine, atunci b = 0 și deci ecuația acestei linii va avea forma y = kx.
Dacă o linie paralelă cu axa Ox, atunci α = 0, și, prin urmare, k = tg α = 0 și ecuația (10.2) ia forma y = b.
Dacă o linie paralelă cu axa y, atunci α = π / 2. ecuația (10.2) devine lipsit de sens, t. k. pantei pentru ea există. În acest caz, ecuația liniei va fi de forma x = a. (10.3)
unde a - abscisa punctelor de intersecție cu axa x. De notat că ecuația (10.2) și (10.3) sunt ecuațiile de gradul I.
Ecuația generală a liniei
Să considerăm ecuația de gradul întâi în raport cu x și y, în forma generală:
în care A, B, C - numerele arbitrare, în care A și B nu sunt simultan zero.
Să ne arată că ecuația (10.4) este ecuația de o linie dreaptă. Două cazuri sunt posibile.
Dacă B = 0, atunci ecuația (10.4) are forma Ax + C = 0, unde A ≠ 0, m. E. X = C / A. Aceasta este ecuația unei linii dreaptă paralelă cu axa y și care trece prin punctul (C / k 0).
Dacă B ≠ 0, atunci din ecuația (10.4), obținem y = -A / Bx-S / B. Aceasta este ecuația unei linii cu panta k = tg α = -A / B.
Astfel, ecuația (10.4) este ecuatia unei linii drepte, se numește ecuația generală a unei linii drepte.
Unele cazuri speciale ale ecuației generale a unei linii drepte:
1) În cazul în care A = 0, ecuația ia forma y = C / V Aceasta este ecuația de o linie paralelă cu axa x;
2) când B = 0, atunci linia paralelă cu axa y;
3) Dacă C = 0, obținem Ax + By = 0. Ecuația satisfac coordonatele punctului O (0, 0), linia dreaptă trece prin origine.
Ecuația dreptei care trece printr-un anumit punct într-o anumită direcție
Substituind valoarea b în ecuația y = kx + b. obținem ecuația dorită a liniei:
Ecuația (10.5) cu diferite valori de ecuații k sunt numite fascicul direct cu punctul central M (xo, yo). Din această rază nu poate fi determinată numai în linie dreaptă paralelă cu axa y.