Prezentarea și o lecție pe tema: „Cum de a construi un grafic al funcției f (x) + m“
Băieți, astăzi vom învăța o altă metodă pentru construirea graficelor de funcții!
Procedăm ca în lecția precedentă, vom construi în același sistem de coordonate trei parabole: $ y = x ^ 2 $, $ y = x ^ 2 + 3 $, $ y = x ^ 2-3 $.
Graficul din prima funcție este bine cunoscut, pentru celălalt construi un tabel de valori. $ Y = x ^ 2 + 3 $.
$ Y = x ^ 2-3 $.
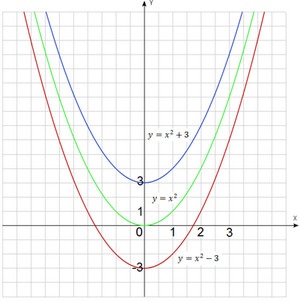
$ Y = x ^ 2 $ - verde, $ y = x ^ 2 + 3 $ - Albastru, $ y = x ^ 2-3 $ - roșu.
Este posibil să observați că grafica sunt practic identice. Toate acestea pot fi obținute de la un parabole convențional deplasat în sus sau în jos. Avem un instrument grafice este aproape identic cu cel care a fost în ultima lecție. Aceasta facilitează construirea de multe alte grafice de funcții.
Scriem regula generală:
Pentru a construi graficul $ y = f (x) + m $, unde $ m $ - a spus numerele pozitive au nevoie de grafic $ y = f (x) $ mutat de unități $ $ m în sus pe ordonată.
Pentru a construi graficul $ y = f (x) -m $, unde $ m $ - a spus numerele pozitive au nevoie de grafic $ y = f (x) $ mutat de $ m $ în jos de unități pe ordonată.
Cu alte cuvinte, în cazul în care se adaugă un număr, graficul este deplasat în sus, în cazul în care se scade, graficul este deplasat în jos.
Exemplul 1.
Construi un grafic al funcției: $ y = -4 x ^ 2 + 2 $.
Decizie.
Programul funcției noastre se obține din graficul de $ y = -4 x ^ 2 $. Acesta este un parabole mutat de către două unități.
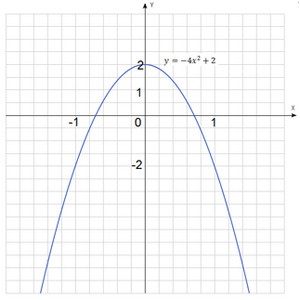
Băieți, să acorde o atenție la scara graficului. O putem alege dumneavoastră, pentru a programa uitat frumos!
Exemplul 2.
Construi un grafic al funcției: $ y = \ frac + 3 $.
Decizie.
Programul funcției noastre se obține din graficul de $ y = \ frac $. Această hiperbolă deplasată cu trei unități în sus.
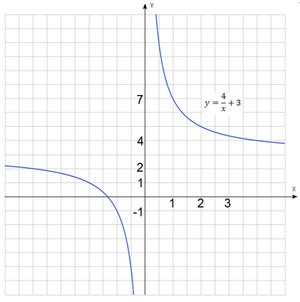
Folosind instrumentul nostru, putem nu numai pentru a construi grafica, dar, de asemenea, rezolva multe alte probleme asociate cu programe.
Exemplul 3.
Găsiți cel mai mic și cel mai mare valoare de $ y = 3 x ^ 2 + 1 $ pe segmentul $ [- 1, 2] $.
Decizie.
Cel mai evident mod de a rezolva acest exemplu este de a construi un calendar adecvat.
Programul funcției noastre se obține din graficul de $ y = 3x ^ 2 $. Acest Parabola deplasat în sus de către o unitate. Evidențiat în intervalul roșu pe care doriți să găsiți valorile minime și maxime. Cel mai scăzut punct al zonei selectate va corespunde cea mai mică valoare, cel mai înalt punct - cea mai mare valoare.
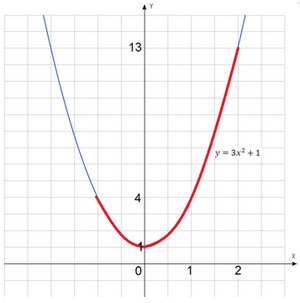
Cel mai jos punct de pe axa Y este egal cu unu, ajungându-se la cel mai înalt punct de ordonata 13. Acestea sunt cele mai mici și cele mai mari valori. $ Y_ = 1 $, $ y_ = $ 13 ani.
Exemplul 4.
Rezolva ecuația: $ x ^ 2 + 1 = \ Frac-2 $.
Decizie.
Noi rezolva ecuația grafic. Noi construim două funcții grafice și pentru a găsi punctul lor de intersecție.
$ Y = x ^ 2 + 1 $ - parabole deplasată în sus de către o singură unitate.
$ Y = \ Frac-2 $ - hiperbolă, deplasate de două unități în jos.
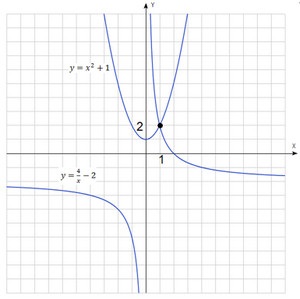
Punctul de intersecție are coordonate $ (1, 2) $. Avem nevoie de coordonatele $ x $.
Raspuns: $ x = 1 $.
Exemplul 5.
Construiți și citiți graficul funcției: $ y = \ începe (x-3) ^ 2, 0Adaugă comentariu
articole similare