Să presupunem că funcția f (t) este definit și continuu la un interval care conține punctul a. Apoi, fiecare număr x în acest interval poate fi asociat cu numărul,
definind astfel funcția interval I (x), care este numit bine definit integralei cu limită superioară variabilă. Rețineți că, la punctul x = a, această funcție este zero. Calculăm derivata a acestei funcții la x. Pentru a face acest lucru, ia în considerare mai întâi incrementarea funcției la x pentru incrementarea argument Dx:
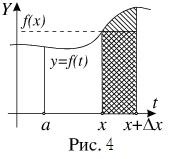
Așa cum se arată în Fig. 4, valoarea din ultima ecuație integrală pentru increment DI (x) este egală cu aria unui trapez curbiliniu marcat de eclozare. Pentru valorile dx mici (aici, precum și în altă parte în acest curs, referindu-se la incrementul mică a argumentului sau a funcției, ne referim la valorile absolute ale incremente ca fac increment poate fi atât pozitive, cât și negative), această zonă este aproximativ egală cu suprafața dreptunghi marcat în dublu ecloziunea figură. Aria dreptunghiului definit de formula f (x) Dx. De aici obținem relația
În ultima egalitate aproximativă a preciziei de apropiere este mai mare, mai mică valoarea Dx.
Formula pentru funcția derivat I (x) Rezultă:
Derivata integrala definită peste limita superioară în punctul x este egal cu valoarea integrantul la punctul x. Prin urmare, funcția primitivă este o funcție f (x), în care un astfel primitiv, care primește la punctul x = valoarea zero. Acest fapt face posibilă introducerea definită ca integrală
Fie F (x) este prea primitiv pentru funcția f (x), apoi prin teorema forma generală a tuturor primitivelor funcției I (x) = F (x) + C unde C - un număr. Partea dreaptă cu formula (1) ia forma
Din formulele (1) și (2) după modificarea x la b formula de calcul integrala definită a funcției f (t) pe intervalul [a, b]:
Se numește formuloyNyutona Leibniz. Aici F (x) - orice funcție primitivă f (x).
Pentru a calcula integrala definită a funcției f (x) pe intervalul [a, b], pentru a găsi orice primitivă F (x) funcția f (x) și se calculează diferența valorilor primitive la punctele b și un. Diferența dintre aceste valori, de obicei, notate cu primitive. și anume .
Înlocuirea unei variabile în definit integral. La calcularea integralele definite folosind formula Newton-Leibniz este, de preferință, nu delimitează rigid pași pentru rezolvarea problemei (găsirea primitive increment integrantul găsirea primitive). Această abordare, utilizând, printre altele, cu formula și înlocuirea variabilei de integrare de către părți pentru o integrală definită, simplifică în general soluțiile de înregistrare.
Teorema. Fie funcția # 966; (t) are un derivat continuu pe intervalul [# 945; # 946;], a = # 966; (# 945;), a = # 966; (# 946); și funcția f (x) este continuă în fiecare punct x de forma x = # 966; (t), unde t [# 945; # 946;].
Apoi, următoarea ecuație:
Această formulă se numește formulă de înlocuire variabilă într-o integrală definită.
La fel cum a fost în cazul unei integrale nedefinită, utilizați schimbarea de variabilă pentru a simplifica integral, aducându-l la masa (tabular). În acest caz, în contrast cu integrala nedefinită, în acest caz, nu este nevoie să se întoarcă la variabila inițială de integrare. Este suficient pentru a găsi limitele de integrare # 945; și # 946; noul t ca variabilă soluția de ecuații de t # 966; (t) = a și # 966; (t) = a. În practică, completarea o schimbare de variabile, de multe ori începe cu acel punct expresia t = # 968; (x) o nouă variabilă prin vechiul. În acest caz, găsirea limitele de integrare în ceea ce privește t este simplificată: # 945 = # 968; (a) # 946 = # 968; (c).
Exemplul 19. Se calculează
Să t = 2 2. Apoi, dt = d (2 x 2) = (2 2) „dx = -2xdx și XDX = - dt. Dacă x = 0, t = 2-0 = 2 2, și când x = 1, t = 2-1 = 1 2. Prin urmare:
Integrarea de piese. Metoda de integrare de către părți ne permite reducerea integrala nedefinită original, într-o formă mai simplă sau realizată integral la masa. Această metodă este cel mai des utilizat, dacă integrantul conține logaritmică trigonometric, exponențială, invers, trigonometrice și combinații ale acestora.
Formula pentru integrarea următoarelor părți.
Aceasta este, integrantul f (x) dx prezent ca produs al funcțiilor u (x) nad (v (x)) - diferențială a funcției v (x). În continuare, vom găsi funcția v (x) (cel mai adesea prin integrare directă) și d (u (x)) - diferențială a funcției u (x). Substituind aceste expresii în formula de integrare prin părți, iar sursa este redusă la o diferență integrală nedefinită. Ultima integrală nedefinită pot fi luate folosind orice metodă de integrare, inclusiv metoda de integrare de către părți.
Ca un exemplu, vom găsi un set de funcții primitivelor logaritm.
Găsiți nedefinită integralei
Să ne găsească nedefinită integralei prin integrarea de părți. Deoarece funcția u (x) ia ln (x). precum și d (v (x)) restul integrantul, adică dx.
Funcția Differential u (x) este. și funcția v (x) - este.
NOTĂ: constanta C, atunci când funcția v (x) este considerat a fi zero.
Acum, tot ce am introdus în formula de integrare prin părți:
.
Cel mai greu lucru din această metodă - este dreptul de a determina ce parte a integrandul ia pentru u (x). și o parte din d (v (x)).
Luați în considerare cazurile standard.
Pentru integralele de forma sau. în cazul în care - polinom de gradul n. a - coeficient ca funcție u (x) polinomul ales.