În diferențierea funcției putere semnificativă sau expresii fracționată voluminoase convenabil de a folosi derivatul logaritmice. În acest articol ne vom uita la exemple de aplicare a acesteia cu soluții detaliate.
Derivarea derivatului logaritmică.
În primul rând logaritmul în baza e. simplificând forma funcției folosind un proprietăți logaritmi și găsiți în continuare derivata funcțiilor implicite:
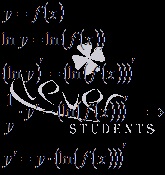
De exemplu, găsim derivatul este un indicator al funcției de putere x la puterea lui x.
Randamentele logaritm. Conform proprietăților logaritm. Diferențierea de ambele părți conduce la rezultatul:

Același exemplu poate fi rezolvată fără utilizarea derivatului logaritmică. Puteți face unele modificări și pentru a trece de la diferențierea este un indicator al funcției de putere pentru găsirea derivata unei funcții compozit:

Găsiți funcția derivat.
În acest exemplu, funcția este o fracție și derivatul pot fi căutate utilizând regulile de diferențiere. Dar, datorită caracterului voluminos de exprimare este un set de transformări necesită. In astfel de cazuri, este rezonabil să se utilizeze formula derivatului logaritmică. De ce? Acum ați înțeles.
Ne găsim mai întâi. Transformarea logaritm va folosi proprietatea (logaritmul fracțiunii este diferența de logaritmi, iar logaritmul produsului este suma logaritmilor, și totuși au un grad de exprimare în logaritm poate fi luată ca un raport al logaritmului):

Aceste transformări ne-au condus la o expresie destul de simplu, derivatul de care poate fi ușor de găsit:
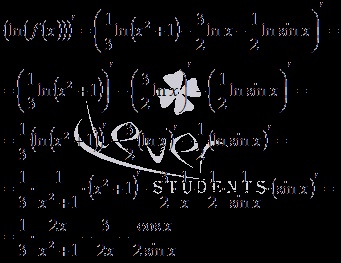
Înlocuind rezultatul în derivatul logaritmică cu formula și a obține un răspuns:
Pentru a consolida materialul vom da câteva exemple, fără explicații detaliate.