Gorbaneva Larisa Valerevna
lector superior în FESUH fizica
Faceți cunoștință cu provocările staticii
condiții studii Statică de echilibru al corpului prin acțiunea forțelor aplicate. Sub echilibru este o stare de repaus sau mișcare uniformă sau rotație. Următoarele tipuri de echilibru: stabil, instabil și indiferent.
echilibru stabil. în cazul în care organismul este dedusă din echilibru stabil, apare forța, se revine la poziția sa de echilibru. Valoarea de echilibru stabil corespunde cu energia potențială minimă.


Un echilibru delicat. în cazul în care organismul este de a se retrage dintr-un echilibru instabil, o forță care îndepărtează corpul din poziția sa de echilibru. Valoarea de echilibru instabil corespunde cu energia potențială maximă.
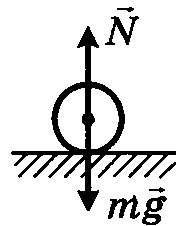
echilibru indiferent. Atunci când organismul care derivă din starea de echilibru neutru apar forțe suplimentare.
Pentru echilibru impune ca suma vectorială a tuturor forțelor exercitate asupra corpului este zero, fie.
Condiția de echilibru poate fi scris în mod diferit. În cazul în care se proiectează toate forțele pe X selectate și axa Y, starea de echilibru devine:
Aceste ecuații sunt numite ecuațiile de echilibru a unui punct material în proiecțiile.
În cazul în care organismul se poate roti în jurul unei axe, atunci nu este suficient de echilibru egal cu zero rezultanta tuturor forțelor.
Acțiunea de rotație a forței nu depinde numai de dimensiunea sa, ci și pe distanța dintre linia de forță de acțiune și axa de rotație.
Lungimea perpendicularei trasată de axa de rotație la linia de acțiune a forței, numită forță umăr. Cel mai adesea umăr notate cu litera d.
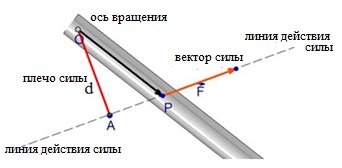
produs modul de putere al umărului D este un punct de putere
. Unitatea de moment de forță - H ∙ m.
Momentul de forță care tinde să se rotească corpul în jurul unei axe de ceasornic este în sens orar pozitiv - negativ.
Dacă organismul are mai multe forțe situate în același plan (sistem plan de forțe), modulul momentului rezultant al forțelor relativ la punctul O selectat este egală cu suma algebrică a momentelor individuale:
momente Regula: un corp având o axă fixă de rotație, este în echilibru, dacă suma algebrică a momentelor forțelor aplicate corpului în jurul acestei axe este zero.
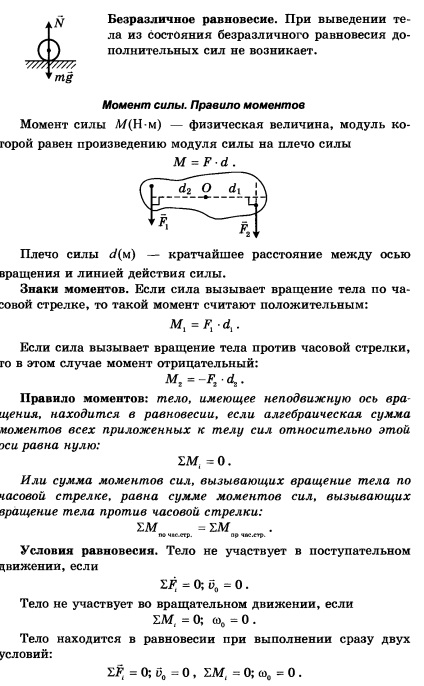
Sau suma momentelor forțelor care provoacă rotirea corpului în sensul acelor de ceasornic, este egală cu suma momentelor de forțe care cauzează corpului de rotație invers acelor de ceasornic:.
Pentru echilibrul corpului necesită două condiții:
Suma vectorială a tuturor forțelor aplicate unui corp este egal cu zero.
Suma algebrică a cuplurilor în jurul oricărei axe este zero.
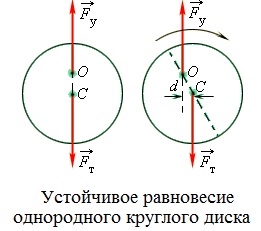
Pentru un corp având o axă de rotație fixă, toate cele trei tipuri de posibile echilibru. echilibru Indiferent are loc atunci când axa de rotație trece prin centrul de masă. Atunci când centrul de echilibru stabil și instabil de gravitație este pe linia verticală care trece prin axa de rotație. Aici, în cazul în care centrul de greutate este sub axa de rotație, echilibrul este stabil. În cazul în care centrul de masă este situată deasupra axei - (. Vezi figura) starea de echilibru instabil.
Un caz special este echilibrul organismului pe suport. În acest caz, atașat nu la un punct forța elastică a suportului și distribuite pe baza corpului. Corpul este în echilibru, dacă linia verticală trasată prin centrul de masă al corpului, trece prin zona de lagăr, adică. E. In cadrul buclei formate de liniile care leagă punctele de sprijin. Dacă această linie nu se intersectează zona de contact, corpul este înclinat. Un exemplu interesant al echilibrului corpului pe suport este Turnul din Pisa în orașul italian, care, conform legendei, Galileo utilizat în studiul legilor organismelor care se încadrează liber. Turnul are o înălțime de cilindru 55 m și o rază de 7 m. Partea superioară a turnului este înclinată față de verticală cu 4,5 m.
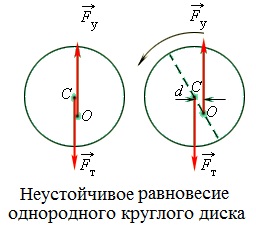
O linie verticală trasată prin centrul de masă al turnului, intersectează baza de aproximativ 2,3 m de centru. Astfel, turnul este într-o stare de echilibru. Equilibrium este perturbată, iar turnul va cădea atunci când abaterea de sus de la verticală ajunge la 14 m. Aparent, acest lucru se va întâmpla foarte curând.
Pentru a rezolva problemele staticii pot folosi algoritmul.
1. Asigurați-un desen pentru a arăta toate forțele care acționează asupra corpului (sau sisteme ale organismului), care sunt într-o poziție de echilibru, pentru a alege un sistem de coordonate și de a determina direcția axelor de coordonate.
2. Pentru corp care are o axa de rotație, prima condiție este scris în formă vectorială echilibru. apoi înregistrează starea de echilibru în proiecțiile pe axele de coordonate și pentru a obține o ecuație în formă scalară.
3. Pentru corp, cu o axă fixă de rotație, este necesar să se definească umerii tuturor forțelor în jurul acestei axe și de a folosi oa doua condiție de echilibru (de obicei, punctele).
În cazul în care problema condiției ca axa de rotație a corpului nu este fix, este necesar să se utilizeze atât condițiile de echilibru. Pentru a face acest lucru, selectați axa cu privire la care este indicat să se determine cuplul (poziția axei de rotație trebuie să fie aleasă astfel încât acesta a trecut prin cel mai mare număr de linii de acțiune a forțelor necunoscute), pentru a determina umeri rezistență și scrie o ecuație care exprimă a doua condiție de echilibru.
4. Pentru a rezolva sistemul de ecuații rezultat pentru a determina cantitățile necunoscute.
Luați în considerare exemplele de rezolvare a problemelor cu utilizarea algoritmului prezentat mai sus.
Exemplul 1. Un cilindru de cântărire m = 150 kg este reținut pe un plan înclinat cu bandă, cu o parte montată pe un plan înclinat, iar cealaltă paralelă îndreptată spre planul. Găsiți forța de tracțiune a benzii. Unghiul de înclinare a planului de a = 30 °.
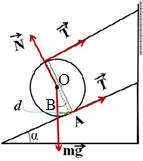
Decizie. Problema poate fi rezolvată folosind fie doar prima condiție de echilibru, sau numai al doilea.
1 mod. Folosind prima condiție de echilibru. Scriem suma tuturor forțelor care acționează. unde T - forța de întindere a benzii, N - forța de reacție a podelei, mg - forța de gravitație cilindru.
Ia proiecția forțelor pe OX și OY. Directă axa OX-a lungul forței de tensionare bandă și axa OY perpendicular pe axa selectate și în direcția forței N.
Rezolvarea sistemului de ecuații rezultat pentru T obținem:
2 metodă. Aplicabile în mod tipic momente în jurul unei axe care trece prin punctul A.
Umăr gravitație d1 este determinată din triunghiului OAB unde OA = R. unghiul AOB egal cu unghiul de înclinare a planului. Apoi d1 = R · sinα.
cureaua de forța de tensionare d2 este diametrul cilindrului sau d2 = 2R.
Apoi regula momentelor în jurul axei A:
Din această ecuație, obținem:
Exemplul 2. Un fascicul subțire omogenă AB cântărind 100 kg este susținută la un capăt pe o podea orizontală netedă, iar cealaltă - pe planul neted înclinată la un unghi de 30 ° față de orizontală. Capătul susținut al grinzii cu coarda de încărcare atârnată deasupra blocului C (vezi Fig..). Se determină greutatea mărfurilor și forța de reacție a podelei plan normal și înclinat. Neglijarea frecare în bloc.
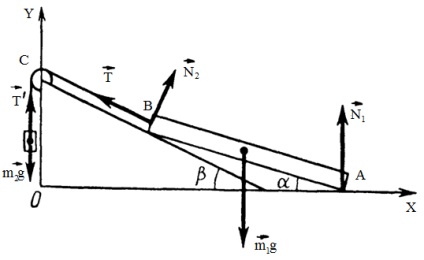
Decizie. Luați în considerare forțele care acționează pe grinda: M1G - forța de gravitație; N1 și forța de reacție normală podea N2- și planul înclinat; T - forță de tracțiune coarda.
Sub influența acestor forțe fasciculului este în echilibru. Scrie pentru grinzi prima stare de echilibru:
Prin alegerea direcția axelor OX și OY (așa cum se arată) proeminente pe ele ecuație, obținem
Scriem grindă a doua condiție de echilibru în raport cu o axă care trece prin punctul B: M1 M2 = 0.
Substituind expresiile pentru M1 și M2 se obține
în cazul în care. Substituind date numerice obține N1 = 490N.
Substituind această expresie în ecuație. și folosind ecuația
Deoarece sarcinile sunt în echilibru, atunci. și.
Apoi. Substituind date numerice m2 = 25 kg.
Substituind expresia pentru N2 T valoarea găsi.
Exemplul 3. Ladder taxa 4m peretelui perfect netedă, la un unghi de 60 ° față de orizontală. Coeficientul de frecare dintre pardoseli și scări 0.33. Cât de departe de-a lungul scării poate urca o persoană înainte de scara începe să alunece? scara de greutate neglijate.
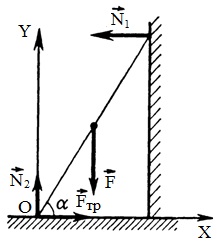
Notăm toate forțele care acționează pe scara: N1 și N2 - forța de reacție este perete și podea, F - forța presiunii umane pe scări; FTP - forța de frecare.
scări glisante pot fi considerate ca o combinație a două mișcări: o rotație (în jurul punctul O) și înainte (în direcția axei față X).
Scriem prima condiție de scara de echilibru:
Noi prognozăm ecuația rezultată
Scriem a doua condiție a scării în raport cu punctul de echilibru A:
Luând în considerare acest lucru, putem rescrie echilibrul condiție scara în jurul punctului O.
Din această ecuație.
Folosind ecuația primei condiții scării de echilibru și de determinare precum și forța de frecare găsi N1 = pF.
Substituind datele numerice obținute S≈2,3m.
Examinarea pentru elevii din clasa a 9.
F.9.1. fascicul Omogene de 6 metri la capetele lor se bazează pe doi piloni. Pentru fasciculul la o distanță de 2 m de la capătul din dreapta al masei suspendate a sarcinii m = 750 kg. fascicul de masa 120 kg. Cu ce fascicul de forță cu presiunea de sarcină pe suportul din dreapta?
F.9.2. Pe teren se afla un fascicul cântărind 90 kg. Ce forță trebuie aplicată pentru a ridica fasciculul într-unul din capetele sale?
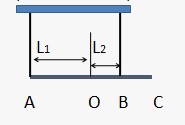
F.9.3. masa fasciculului este suspendat pe 140 kg de două frânghii. Se determină cablurile de forță de tensiune dacă L1 = 3m, L2 = 1m.
F.9.4. Dacă montați două mase de marfă 2m și m pe o tijă fără greutate de lungime L = 3m. așa cum se arată în figură, apoi, la tija a rămas în echilibru, acesta trebuie să fie agățată într-un punct situat la O distanța x de la o masă de 2m. Găsiți distanța x.

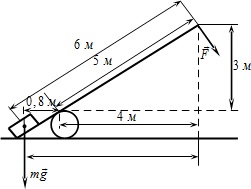
F.9.5. Sub influența gravitației mg de sarcină și forța pârghiei F, prezentată în figură, este în echilibru. Vectorul forță F este perpendiculară pe brațul. Distanța dintre punctele de aplicare a forței și punctul de sprijin, precum și proiecția acestor distanțe în axa verticală și orizontală este indicat în figură. Localizați modulul de gravitație care acționează asupra sarcinii, în cazul în care forța F este 120 N module.
F.9.6. O pârghie atașată la capetele forței îndreptată în jos și 6 H 4 N. Punctul de sprijin este situat la 5 cm mai aproape de un capăt al pârghiei decât în cealaltă. Care este lungimea (cm) a pârghiei atunci când este în echilibru?
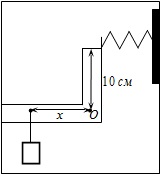
F.9.7. Pârghie Lung formă complexă, cu punctul de rotație la un punct O (vezi. Figura) este suspendat de o greutate de 2 kg și un arc este atașat, al cărui al doilea capăt este atașat la perete fix. Pârghia este în echilibru, iar tensiunea forței arcului este de 15 N. La o oarecare distanță de axa de rotație x sarcină suspendate, în cazul în care distanța de la axa la punctul de atașare al arcului este de 10 cm.
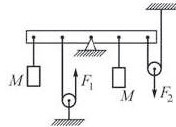
F.9.8. Pentru a echilibra pentru metroul ușor prin intermediul a două sarcini identice blocuri fara greutate fiecare masa M la firul aruncat peste un bloc de la stânga la dreapta și blocul osiei trebuie să aplice forțele verticale F1 și F2 (vezi. Figura). Distanța dintre punctele negre de pe șină sunt la fel, nu există nici o frecare, fire neextensibil. Ce se poate argumenta despre F1 și F2 forțele.
F.9.9. Sistemul de mase m și M, și conectarea lor fir inextensibil lumină în momentul inițial de repaus într-un plan vertical care trece prin centrul sferei este fixat. Load m este la punctul A de pe partea de sus a sferei (vezi. Figura). În timpul mișcării de marfă a apărut m separate de suprafața sferei care trece prin ea un arc de 30 °. Localizați masa m când M = 100g. Dimensiuni sarcină m este neglijabilă în comparație cu raza sferei. Frecare neglijate.
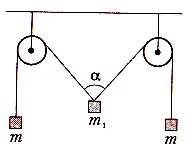
F.9.10. La capetele filamentului, slung peste două blocuri, două sarcină identice suspendate în masă de 5 kg fiecare. Care este greutatea sarcinii are m1. când la echilibru a = 120 °?
F.9.11. Stairway se află pe un perete vertical și podea orizontală. Coeficientul de frecare dintre scării și peretele 0.5. și între etaje și scara - 0.4. Determina cel mai mic unghiul de înclinare al scării în care poate fi încă în echilibru.
F.9.12. Tija cântărind 9 kg și 1 m lungime se intinde pe doua suporturi. Unul susține capătul din stânga al barei, iar celălalt este situat la o distanță de 10 cm de la capătul din dreapta. Cu ce acte vigoare la fiecare dintre pilonii de bază? Ca răspuns pentru a înregistra forțele de diferență.
F.9.13. tijă din oțel cu o greutate de 6 kg este încorporat într-un perete de capăt și este susținut la punctele A și B; la celălalt capăt în punctul C este suspendat de o greutate de 36 kg. Găsiți o forță de presiune asupra suportului de la punctele A și B, în cazul în care lungimea tijei 80cm. și lungimea proeminentă 60 cm.
F.9.14. Staircase cântărind 1,5 kg rezemat pe un perete vertical, la un unghi de 300. Centrul de greutate al scării este situat la 1/3 din lungimea capătului său superior. La capătul de sus al scării nu pune presiune pe perete la mijlocul scărilor este necesar să se aplice o forță îndreptată orizontal. Se determină valoarea acestei forțe.
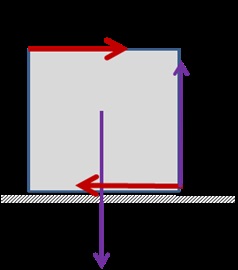
F.9.15. Care este forța orizontală minimă poate fi răsturnată prin cubul de margine, situată pe un plan orizontal?
Documente conexe:
și 01 septembrie 08 septembrie Indice 531.2 arta resheniyazadachpo conține exemple: reacții de relații care determină plat. POSTATIKE PROFIL ANEXA. NECESARE PENTRU RESHENIYAZADACH 1. Comunicare și. Relații) În studiul unei resheniizadachpostatike rigide.
time-dimensiuni, grafice și așa soluții. d. dinamică și statică (8 h) Coordonata Metoda mecanica resheniyazadachpo. Resheniezadach pe legile de bază.
condiții de echilibru solide. Algoritmul resheniyazadachpostatike. Exemplele resheniyazadach. 04 iunie 2.3 Generalizând repetiție. 4.1 Legile electrostatica. Aplicarea resheniyazadachpostatike algoritmul în interacțiunile corpurilor încărcate electric.
curriculum-ul de lucru
sarcini de viață. ETAPA RESHENIYAZADACHPO FIZICĂ Înțelegerea declarația problemă. Asta. energie. Energia mecanică totală. condiții (1 oră) echilibru static și hidrostatică. energie mecanică 9.1-9.45 (1) 12 staticii ianuarie și hidrostatica 10.1-10.26 (1).