Rata de coroziune a metalelor este definit în general viteza de curgere a conjuga reacții electrochimice în potențialul de coroziune:
Când înregistrați curenții parțiale Ecuații necesare pentru a lua în considerare mecanismul detaliat al reacțiilor catodice și anodice în aceste condiții. În unele cazuri, ecuația vitezei de coroziune poate fi redus la forma icor = ik2 = IA1 (unde ik2 - regenerare oxidant; IA1 - viteza de dizolvare metal) al acestuia obținut expresie pentru potențialul de coroziune și pentru viteza procesului de coroziune.
Să presupunem că viteza ambelor procese este limitată prin etapa de transfer de electroni. apoi:
Transformarea acestei ecuații, obținem:
Astfel, cunoscând valoarea măsurătorilor cinetice # 945; * și k2 # 945; * a1. puteți obține dependența potențialului de coroziune al concentrației de oxidant. Substituind expresia pentru Ekor în ecuația anterioară, găsim viteza de coroziune a unui metal (densitatea curentului de coroziune)
Ecuația obținută prin potențiale identice de expresie la coroziune Tial substituite în partea dreaptă a ecuației pentru rata de coroziune.
Din ecuațiile care
în cazul în care se obțin valori # 945; * și k2 # 945; * a1.
Să considerăm acum un exemplu specific al coroziunii zincului în soluții acide. Deoarece rata de evoluție a hidrogenului la zincul este limitată de etapa de transfer de electroni și # 945; * k2 = # 945; k2 = 0,5, iar viteza de dizolvare a zincului - etapa de clivaj al doilea electron, adică .. # 945; * a1 = 1 + # 945; a1 = 1,5, (la # 945; a1 = # 945; k2 = 0,5), atunci ecuația vitezei de coroziune poate fi scrisă ca:
Din ea obținem ecuația pentru potențialul de coroziune:
Astfel, spre deosebire de potențialul de echilibru al electrodului metalic, potențialul de coroziune este independent de ioni metalici ak-getică, dar este dependentă de pH-ul soluției. Această ecuație este bine susținută de date experimentale Liun-Sok, prezentat în Fig. 14.3.
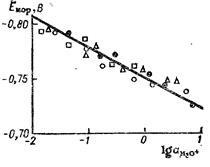
Fig. 14.3. Dependența potențialului de coroziune al electrodului de zinc al logaritmul activității ionului hidroniu.
Diferite puncte corespund diferitelor serii de experimente. Directă a avut loc la valoarea coeficientului unghiular de 0,03.
Substituind ecuația pentru Ekor în ecuație pentru densitatea curentului de coroziune, obținem ultima dependență de aciditatea soluției:
Când coroziunea fierului în rata de soluții de recuperare slab acid de oxidant este limitată de etapa de difuzie (Ya. V. Durdin). Prin urmare, în acest caz, densitatea curentului de coroziune este egală cu limitare ionii de hidroniu de recuperare densitate a curentului și densitatea curentului de ionizare din metal
În consecință, potențialul de coroziune și coroziune densitatea curentului depinde de limitarea curentului și astfel intensitatea soluției sub agitare.
În aceste cazuri, când valoarea de coroziune potențial aproape de potențialul de echilibru al unuia dintre reacțiile electrochimice asociate, rata de coroziune a metalului poate fi calculată prin substituirea expresiilor pentru ecuația potențialului de echilibru în densitatea curentului de coroziune. De exemplu, comportarea la coroziune a amalgamului de sodiu în mediu acid caracterizat prin reacția anodică predominantă
și reacția catodică:
În conformitate cu ecuația pentru densitatea curentului de coroziune, ignorând vitezele de descărcare ale ionilor de sodiu și de ionizare a hidrogenului, putem scrie:
Datorită înaltă schimb densitatea de curent peste amalgam de sodiu și soluții apoase și suprapotențial ridicată a degajării de hidrogen, setează valoarea potențialului de coroziune în eroarea de măsurare este practic identic cu electrod amalgam potențial de echilibru:
Substituind această ecuație în precedent, obținem o expresie pentru rata de descompunere a amalgamului:
Din ecuația rezultă că viteza de coroziune în pH acid rastvopax dependent. Având în vedere că # 945 * k2 ≈ 0,5, obținem o ecuație pentru o constantă și
care, pentru amalgam de metal alcalin în soluții acide confirmate experimental Bronsted și Kane. În soluții cu pH mare (pH> 10), când evoluția hidrogenului are loc ca urmare a descărcării de molecule de apă, viteza de coroziune a amalgamului nu este dependentă de pH-ul soluției.
La schimbarea compoziției soluției este esențială pentru rata amalgamul de descompunere (în special evoluția hidrogenului la catod; .., A se vedea secțiunea 11) oferă o schimbare # 968; „- potențial. Substituind expresia amalgamului în ecuația de echilibru potențial pentru evacuarea ionilor hidroniu sau molecule de apă, cu # 968; „- capacitatea, respectiv, obținem:
Aceste ecuații reprezintă dependența determinată experimental viteza de coroziune a compoziției alcaline amalgam de metal și concentrația soluției și amalgamului până la pH ≈ 10. La rata de descompunere a amalgamului pH mai mare este dependentă liniar de concentrația sa. Pentru o explicație a acestui fapt este prevăzut un mecanism chimic pentru descompunerea amalgamului în soluții alcaline, care se bazează pe presupunerea că o interacțiune directă a amalgamului cu apă:
Rata de descompunere a amalgamului conform acestei reacții
Ea nu depinde de compoziția și pH-ul soluției. Legile pentru mecanism chimic natură LARG, detectate de siliciu sol-reniu alcalin soluții, fier, crom, mangan și oțel crom în acizi (YM Kolotyrkin, T. R. Agladze și angajați).
Viteza de dizolvare a ambelor amalgame de metale alcaline și alcalino-pământoase și metale grele cu coroziune cu conjugatul reacției de evoluție a hidrogenului, în general, poate fi exprimată prin ecuația
unde - rata de descărcare a ionilor hidroniu; - viteza de descărcare a moleculelor de apă; - viteza mecanismului de interacțiune chimică.