Probleme cu - unele dintre cele mai dificile din examen, dar cel mai interesant și. le rezolva - o plăcere. Mi-ar recomanda prietenilor la parametrii și să nu se teamă de provocări.
Sarcină. La ce valoare a parametrului, sistemul are mai mult de două soluții?
Să ne deschide modulul. El va fi împușcat cu un semn pozitiv în cazul în care expresia podmodulnoe este non-negativ și negativ în cazul în care expresia podmodulnoe este mai mică de 0:
Astfel, selectarea unui pătrat perfect, avem două cercuri (sau, mai degrabă, părți ale acestora). Unul dintre cercurile de deasupra liniei de acolo. iar al doilea - de mai jos. O parte din cercurile noastre unite la coordonatele O (0, 0) și C (-2; -4) - este ușor de verificat prin substituție.
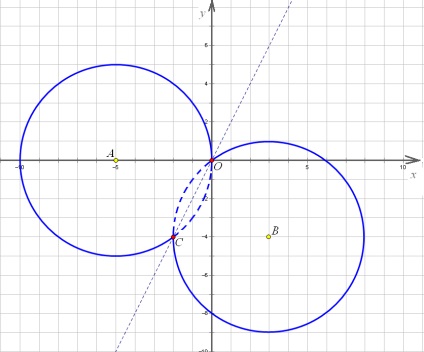
Cercul se va intersecta linia dreaptă a cărei pantă este constantă, iar coeficientul - modificat:
O astfel de linie va aluneca axial în sus și în jos, suntem interesați în cazurile în care această linie va avea mai mult de două intersecții cu „opt“ a cercurilor. Începem cu un studiu al poziției liniei atunci când trece prin origine.
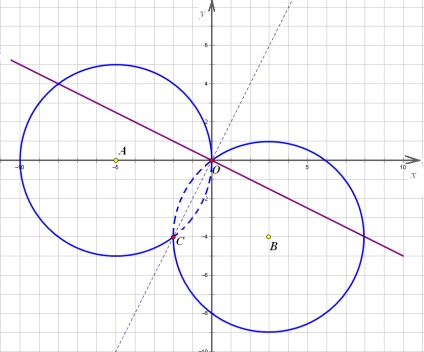
Acesta este un punct extrem la care sistemul are trei soluții. La o poziție inferioară a liniei va fi ceva timp doar de două ori pentru a traversa un cerc (până când atinge punctul C). Dar forfecarea drept în sus de la origine pentru a vedea că intersecțiile din patru - și așa va fi până când linia nu devine o tangentă la cercul. Definim valoarea parametrului dacă originea este dreaptă. pur și simplu, înlocuind coordonatele punctului O în ecuația:
Acum trecem direct noastră în sus până când este tangenta la cercul. În cazul în care poziția liniei va fi în măsură să determine coordonatele unui punct sau punct - truc se face.
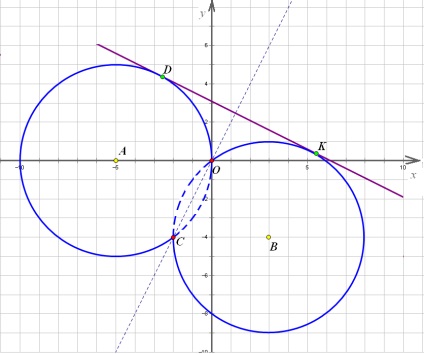
Gândiți-vă: dacă tangenta linia cercului, raza trase la punctul de contact, acesta trebuie să fie perpedikulyaren. Rețineți că drepte. delimitează regiunea existenței cercurilor are o pantă de 2, iar linia - panta. și produsul dintre doi coeficienți este (-1), astfel încât perpendicular directă. Astfel, am demonstrat că linia și linia care aparține raza. au același coeficient de înclinare egal cu 2, adică paralel. Știind că linia ce conține raza. Acesta trece prin punctul. Ne găsim ecuația lui.
Distanța dintre punctele și este cunoscut - este egală cu raza cercului, ele fac parte din aceeași linie, coordonatele sunt cunoscute - nu costă nimic pentru a găsi coordonatele.
Să ne rezolve prima ecuație pătratică a sistemului:
Două rădăcini - coordonatele punctelor de pe axa și punctul opus - vom avea nevoie de ea mai târziu, și ne vom întoarce la ea.
Suntem acum în căutarea unui parametru, înlocuind coordonatele punctului în ecuația liniei:
Noi o mică victorie: am găsit unul din gama de parametri care ne-ar potrivi:
Zero intră în acest interval, pentru că există trei puncte de trecere, dar a doua limita - nu va merge în jos, există doar două puncte de contact și au nevoie.
Începând cu a doua constatare gama:
În mod similar, pur și simplu, înlocuind ecuația coordonatele punctului, determinăm valoarea parametrului în cazul în care o trecere directă prin acest punct:
Iată acum este ceea ce ne întoarcem la a doua soluție a ecuației de gradul doi: este - coordonata axei punct. .
Apoi coordonata pe axa Y:
Noi determinăm valoarea parametrului:
Apoi, al doilea interval al valorilor parametrilor este :.