
Gauss - o metodă clasică pentru rezolvarea unui sistem de ecuații algebrice liniare (Slough). Luați în considerare sistemul de ecuații liniare cu coeficienți constanți valide:
sau sub formă de matrice
Metoda Gauss pentru rezolvarea ecuațiilor liniare include două etape:
- secvențială excludere (directă);
- substituție inversă.
excepție consecventă
eliminarea gaussiană se bazează pe ideea de variabile secvențiale excepția unuia, atât timp cât va exista doar o singură ecuație cu o singură variabilă pe partea stângă. Apoi, această ecuație este rezolvată pentru o singură variabilă. Astfel, sistemul de ecuații conduce la un triunghi (în trepte) mod. Pentru această primă coloană printre elementele selectate ale matricei nenuli (și adesea maxim) elementului și se trece la cel mai de sus permutarea rând poziție. Apoi, toate ecuațiile sunt normalizate prin împărțire prin coeficientul AI1. unde i - numărul coloanei.
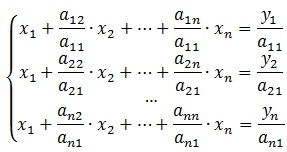
Apoi se scade rezultând după rearanjarea primul rând din rândurile rămase:
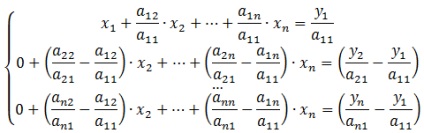
Ia un nou set de ecuații, care sunt înlocuite cu coeficienții corespunzători.
Odată ce aceste transformări au fost realizate, primul rând și prima coloană și mental eliminându-se continuă procedeul respectiv pentru toate ecuațiile următoare până nu ecuație într-o singură necunoscută:
Contactați înlocuirea
Contactați substituția implică substituția obținută în etapa anterioară, valoarea variabilei xn în ecuația anterioară:
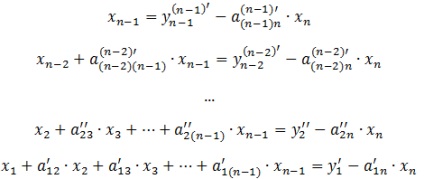
Această procedură se repetă pentru toate deciziile rămase:
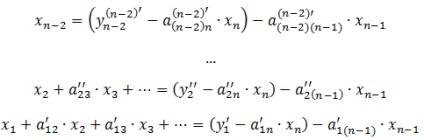
care ilustrează un exemplu de
Având în vedere un sistem de ecuații
sau sub formă de matrice
Alegeți linia cu cel mai mare coeficient de AI1 si schimba-l din prima.
Noi normaliza ecuația pentru coeficientul de x1:
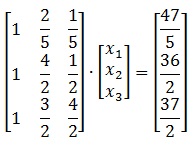
Scădeți 1 din ecuația 2 și 3:
Alegerea unui șir cu cel mai mare coeficient de AI2 (ecuația 1 nu este considerată) și mutați-l în locul 2.
Normaliza ecuațiile 2 și 3 în ceea ce privește coeficientul de x2
Scădeți 2 din ecuația 3
Noi normaliza ecuația 3 în ceea ce privește coeficientul de x3
Cum obținem x3 = 2. Înlocuim valoarea obținută în ecuațiile 1 și 2 obținem
Substituind această valoare x2 = 5 în ecuația 1, obținem
Astfel, rezolvarea sistemului de ecuații este vectorul
Implementarea în C ++
#include
using namespace std;
// Afișarea sistemului de ecuații
void sysout (dublu **, cu dublu * y, int n)
pentru (int i = 0; i
>
cout <<" = " <
return;
>
double * gauss (double ** a, dublu * y, int n)
double x *, max;
int k, indicele;
eps duble const = 0,00001; // precizie
x = new double [n];
k = 0;
în timp ce (k
max = abs (a [k] [k]);
index = k;
pentru (int i = k + 1; i
max = abs (a [i] [k]);
index = i;
>
>
// permutare rând
în cazul în care (max
cout <<"Решение получить невозможно из-за нулевого столбца " ;
cout <
>
pentru (int j = 0; j
o [k] [j] = a [index] [j];
o [index] [j] = temp;
>
double temp = y [k];
y [k] = y [index];
y [index] = temp;
// Ecuațiile de normalizare
pentru (int i = k; i
if (abs (temp)
y [i] = y [i] / temp;
în cazul în care (i == k) continuă; // ecuație nu se scade din ea însăși
pentru (int j = 0; j
y [i] = y [i] - y [k];
>
k ++;
>
// inversă substituție
pentru (k = n - 1; k> = 0; k--)
x [k] = y [k];
pentru (int i = 0; i
>
întoarce x;
>
int main ()
duble ** a, * y, * x;
int n;
sistem ( "chcp 1251");
sistem ( "cls");
cout <<"Введите количество уравнений: " ;
>> n cin;
a = new double * [n];
y = new double [n];
pentru (int i = 0; i
pentru (int j = 0; j
Soluția sistemului de ecuații liniare în ms Excel - studopediya