Atunci când se planifică activități extracurriculare, am stabilit un obiectiv: de a apela interesul elevilor în acest subiect. Electives contribuie la dezvoltarea Outlook matematice, capacitatea creativă a elevului, promovarea abilităților de lucru independente și pentru a îmbunătăți astfel calitatea pregătirii matematice a studentului.
Acest curs electivă a avut loc în clasa a 9-a după subiecte care studiază cum ar fi repetor-sinteza, care permite nu numai să rezume și să consolideze cunoștințele lor. La această sesiune am invitat 10 participanți 7 clase în care lucrez (inclusiv 2 co-raportor).
Subiect: „Metode pentru sisteme de ecuații de rezolvare.“Tipul de lecție - o conferință de presă.
- căutare pentru diverse căi și metode de sisteme de ecuații de rezolvare, abilitatea de a vorbi în fața unui public cu un mesaj pregătit.
- stimulează metode non-standard de gândire creativă.
- generalizarea și sistematizarea cunoștințelor elevilor cu privire la acest subiect, predau lucru cu ajutorul și literatura suplimentară.
- dezvoltarea gândirii matematice, sprijin reciproc, ajutor reciproc, precum și capacitatea de a conduce o dezbatere culturală, limbajul matematic corect.
- ridica simțul responsabilității.
Echipament: afișe, tabele, diagrame, carduri - a se vedea apendicele 1
Panel: profesor, părinte, elev.
Ordinea de zi (a planului de conferințe):
- Mesajul 1. Din istoria sistemelor de ecuații de rezolvare / Ogloblina OS / Grad 9
- Mesaj 2. Sistemele Rezolvarea prin substituirea / D. Khokhlov / Grad 9
- 3. Mesaj Sisteme ecuații simetrice / Troyanova K / 9 Clasa
- 4. Sisteme post de ecuații liniare cu parametri / Zablocki AN / Grad 7
- Post 5. Metodele geometrice ale sistemelor de ecuații / VV Kravets rezolvare / Grade 9
- 6. Mesaj Cramer regulă sau metoda determinanților / Trifonov RO / 9 clasa
Munca creativă - problema ziarului de perete „News de la conferința“
Din istoria sistemelor de ecuații de rezolvare.
Acesta a fost mult timp excepția în necunoscutul ecuații liniare. În XVII - XVIII Tehnici de excludere a dezvoltat agricole, Newton, Leibniz, Euler, Bézout, LaGrange (portrete este expus la birou).
În sistemul de înregistrare modernă a două ecuații liniare cu două necunoscute este după cum urmează:
Soluția acestui sistem este exprimat prin formulele
Datorită metodei de coordonate, stabilit în secolul al XVII-lea. Fermat și Descartes, a fost posibil pentru a rezolva sisteme de ecuatii grafic.
În textele scrise în caldeeni III - II milenii î.Hr. Acesta conține o mulțime de probleme care trebuie rezolvate cu ajutorul elaborării sistemelor de ecuații, care include ecuațiile de gradul al doilea. De exemplu, numărul de sarcină 20. pătrat sale două pătrate am pus: 25. Partea a doua parte a pieței este primul și încă 5. Sistemul corespunzător de ecuații în înregistrare modernă este:
înlocuind obține 1 x 2 + x = 6, rezolvarea ecuației, găsim x, atunci y.
Diophant, care nu avea denumiri pentru multe necunoscute, a făcut eforturi mari pentru a selecta un mod necunoscut de a reduce soluția la rezolvarea sistemului de ecuații.
Problema 21. „găsi două numere întregi pozitive, știind că suma lor = 20, iar suma pătratelor 208“.
Problema rezolvată ca ecuațiile sistemului,
dar Diofant rezolvate prin selectarea ca jumătate din diferența de numere unknown unknown, care
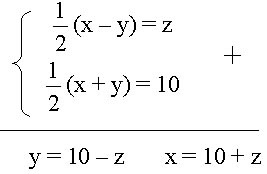
x 2 + y 2 = (z + 10) 2 + (10 - z) 2 = 2z + 2 200, și cu condiția = 208
z = ± 2 z = - nu 2- bătăi. Condiții. sarcini
cu toate acestea, în cazul în care z = 2 x = 12 și y = 8.
Soluție sisteme de metoda de substituție.
Cu sistemele de ecuații, ne-am întâlnit în cursul algebra în clasa a 7-a, dar a fost un tip special de sistem - un sistem de două ecuații liniare cu două variabile
Algoritmul, care a fost dezvoltat în clasa a 7-a, este destul de potrivit pentru sisteme de oricare două ecuații de rezolvare în două variabile x și y.- Exprimă în ceea ce privește x al unui sistem de ecuații.
- Substituind expresia y în cealaltă ecuație a sistemului.
- Pentru a rezolva ecuația rezultată pentru x.
- Substitut alternativ fiecare găsit în pasul 3 în loc de rădăcinile x în y expresie prin x, obținut în prima etapă.
- răspuns înregistrare sub formă de perechi de valori (x, y).
Am arată modul în care această metodă în rezolvarea unor sisteme mai complexe. / V. Kravets /
x 2 - xy - 2y 2 = 0
Noi rezolva ecuația rezultată în ceea ce privește x
A = y2 - 4 1 • (- 2y2) = 9u2. = 3 | y |
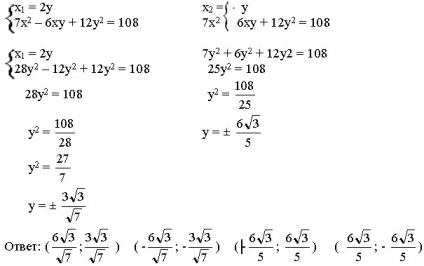
Soluție de sisteme simetrice de ecuații.
Există o metodă de soluție universală: de substituție introdusă
Noi transformăm prima ecuație a sistemului, adăugând la ambele părți ale xy
x 2 + xy + xy + y 2 + xy = 4
2xy + x 2 + y 2 + xy = 4
Aplicăm schimbarea universală
Luați în considerare soluția unui alt sistem

(X + y) 5 = x 5 + 5x 4 y + 10 x 3 y 2 + 10x 2 y 3 + 5xy 4 + y 5 = (x 5 + y 5) + 5xy (x 3 + y 3) + 10x 2 y 2 (x + y)
x 3 + y 3 = (x + y) 3 - 3hu (x + y), folosind formula (2)
5 5 = 275 + 5z • Pot 3 - 15z 2 • 5 + 10z 2 + 5 /. 25
May 3 = 11 + 25z - 3z 2 + 2z 2. z 2 - 25z + 114 = 0
Sistem de ecuații liniare cu un parametru
Permiteți-mi să vă reamintesc exemple de trei cazuri:
a) când coeficienții x și y nu sunt proporționale cu
b) atunci când rapoartele sunt proporționale
c) coeficienții x este proporțional cu coeficientul de y, dar nu proporțional cu membrii liberi.
Această cunoaștere este esențială în rezolvarea următoarelor sarcini:
* Identificarea tuturor valorilor unui pentru care sistemul de ecuații

O metodă geometrică pentru sistemele de ecuații de rezolvare
Prin teorema lui Pitagora inversa teorema, ecuația x 2 + y 2 = 3 2. Numerele x și y sunt picioarele ABD (D - line) cu ipotenuza AB = 3.
Luând în considerare a doua ecuație y 2 + z 2 = 16 construct BDC, unde y și z - picioare, și BC = 4 - ipotenuza.
A treia ecuație y = xz 2 sugerează că numărul y este proporțional cu media numerelor x și z.
Prin segmentele proporționale inverse teorema Teorema ABC = 90 0
AC = (x + z) = = 5,
Apoi, AB 2 = AD • AC, 9 = x • 5 x =
BC 2 = DC • AC, 16 = z • 5, z =
BD 2 = y 2 = x • z = ·
Această tehnică oferă pierderea de rădăcini, ușor de a face,
că x = ± 9/5; y = ± 12/5; z = ± 16/5.
Pentru un sistem de referință dat poate fi și altele.
De exemplu, ceea ce este valoarea expresiei
xy + ux; x + y + z; x + y; x + z;
tip de sistem este numit un sistem de două ecuații liniare cu două necunoscute, unde a1; a2; B1; B2; C1 și C2 - număr. Și a1 + c1 2 2 0 2 a2 + c2 2. 0.
Una dintre principalele metode de rezolvare a acestui sistem este metoda de metoda Kramer sau determinanților. Coeficienții acestui sistem este de trei factori determinanți: (principal), x - x determinant necunoscut; y - determinantul y necunoscut.
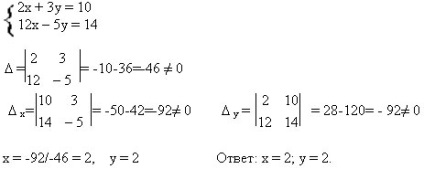
* Gaseste toate valorile parametrului b, pentru care sistemul are o soluție unică

Munca creativă pe carduri vzaimotrenazhera „Desenează coordonate.“
Rezolva sistem și de a construi o figură în coordonatele.
Conferința sa încheiat. Cred că aveți o dorință de a încerca mâna la sistemele de rezolvare a problemelor. Ia locul de muncă și de a ajunge la munca de creație.
Și acum a venit timpul de a emite următoarea ediție a ziarului matematic „News de la conferința“.
1. GI Glaser, „Istoria matematicii la școală“
2. IJ Depman „pe pagină algebra manual“
3. ML Galitsky A.M.Goldman "Probleme în Algebra 8-9"
4. AG Mordkovich "Algebra 9". "Algebra 7"
5. YN Makarychev "Algebra 9". "Algebra 7"