
Din nou ... trigonometrie! Din nou, aceste formule de memorare fără sfârșit. Formule de reducere reprezintă aproximativ 32 de biți (!) bucăți! La fel de ușor să vă amintiți formula pentru a aduce?
DAR! O să-ți spun imediat: să leșin și disperare - nu-l merita! Aici am vă va solicita „cheie“ destul de simplu sau regulile de eliminarea acestor formule. Asta este, să-i învețe - să nu-l merita!
Permiteți-mi să vă reamintesc că funcțiile date au forma:
$ Latex \ displaystyle păcat \ stânga \ (\ fracn \ pm \ alpha \ dreapta), \ \ cos \ left (\ fracn \ pm \ alpha \ dreapta), \ tg \ left (\ fracn \ pm \ alpha \ dreapta), \ ctg \ stânga (\ fracn \ pm \ alpha \ dreapta), unde $ $ latex \ displaystyle n $ - întreg
Să începem. Nu să memoreze toate formulele din distribuție, trebuie să învețe două etape:
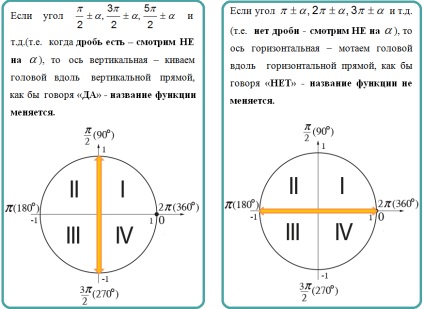
Sign pe partea dreaptă la fel ca și funcția inițială este familiarizat cu condiția ca unghiul de $ latexul \ displaystyle \ alpha $ - acute (mai puțin de 90 de grade). Semnul funcției inițiale este ușor de a determina printr-un cerc trigonometrice.
Pentru a determina dacă numele funcției este modificată la kofunktsiyu (adică sinus - cosinus, și invers, precum și tangentă la cotangentă, și vice-versa). Pentru acest lucru suficient pentru a determina pe care axa - orizontal sau vertical - unghi întârziat.
De exemplu, sarcina noastră este de a găsi valoarea expresiei:
$ Latex \ displaystyle \ păcat \ stânga (\ frac \ dreapta) $
Pentru a începe, vom da o expresie de obicei pentru noi înseamnă $ latex \ displaystyle \ păcat \ stânga (\ fracn \ pm \ alpha \ dreapta) $ și aruncați numărul de rotații complete de $ latex \ displaystyle 2 \ pi $:
Ei bine, trecem la utilizarea noastre două reguli (pași):
- Noi determina semnul funcției originale. în unele sferturi este unghiul $ de latex \ displaystyle \ Frac + \ frac $?
$ Latex \ displaystyle \ frac + \ frac $ - este unghiul $ latex \ displaystyle IV $ sferturi. Sinusul unghiului $ latex \ displaystyle IV $ trimestru - mai putin de zero! Prin urmare, semnul stabilit dreptul de curaj «$ latex \ displaystyle - $»!
- Pentru a răspunde la întrebarea dacă schimbarea denumirii funcției la kofunktsiyu.
Acesta poate răspunde imediat:
$ Latex \ displaystyle \ Frac + \ frac $ - fracțiune au $ latex \ displaystyle \ rightarrow $ nods din cap. „DA“ - numele este schimbat, adică, schimbarea sinus și cosinus!
Depășirea acestor două etape, putem scrie în siguranță soluția:
$ Latex \ displaystyle \ păcat \ stânga (\ Frac + \ frac \ dreapta) = - \ cos \ frac = - \ frac> \ \ \ din stânga (* \ dreapta) $
$ Latex \ displaystyle \ stânga (* \ dreapta) $ - (! Trebuie să ne amintim) această valoare tabel
Este activat! Pe nas de Anul Nou! Înainte de examenele de foarte puțin timp - pentru a aprecia avantajele formării cu YouClever.org!
Mult noroc la examene!