Acasă | Despre noi | feedback-ul
sistem de trei axe ordonata reciproc perpendiculare, cu o referință comună de pornire (de origine), iar lungimea totală a unității se numește un sistem de coordonate cartezian rectangular în spațiu.
În acest sistem ordonata axe de coordonate 0xyz axa Ox se numește axa orizontală. axa 0Y - axa y. iar axa 0Z - axa z.
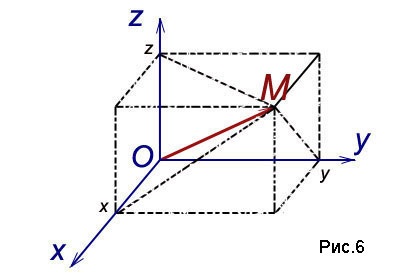
numit vectorul raza punctului M și proiectează-l pe fiecare dintre axele de coordonate. Notăm valori proiecții corespunzătoare:
Numerele x, y, z coordonatele punctului M. numit respectiv abscisei, ordonata si applicate. și este scris într-un numere de puncte ordonate: M (x, y, z) (Fig.6).
versorul a cărei direcție coincide cu direcția axei, se numește un vector unitate (sau vector unitate) axă. Vom nota cu
Prin urmare, vectorii unitare ale axelor de coordonate Ox. Oy. oz
Teorema. Orice vector poate fi descompus prin unități vectorii axelor de coordonate:
Ecuația (2) se numește vectori de descompunere a lungul axelor de coordonate. Coeficienții acestei extinderi sunt proiecții ale vectorului pe axele de coordonate. Astfel, coeficienții de dilatare (2) al vectorului pe axele de coordonate sunt coordonatele vectorului.
După selectarea unui sistem de coordonate anumit vector spațiu și originea triplu determină în mod unic reciproc, cu toate acestea, vectorul poate fi scrisă sub forma
Reprezentarea Vector in forma (2) și (3) sunt identice.
Condiția de coliniaritate a vectorilor în coordonate
Așa cum am observat, vectorii se numesc coliniare în cazul în care acestea sunt legate de
Să presupunem că vectorii. Acești vectori sunt coliniari, dacă coordonatele vectorilor sunt legate de
adică, coordonatele vectorilor proporționale.
Exemplul 4 Date fiind vectorii. dacă acești vectori sunt coliniari?
Decizie. Să ne determine raportul dintre vectorii de coordonate de date:
Coordonatele vectorilor proporționale, prin urmare, vectorii sunt coliniari, sau ceea ce este același paralel.
Datorită lungimii axelor perpendiculare reciproc vector
este lungimea diagonalei unui paralelipiped rectangular construit pe vectorii
și este exprimată prin ecuația
Vectorul este complet determinată prin două puncte (pornire și de oprire), astfel încât coordonatele vectorului pot fi exprimate prin coordonatele acestor puncte.
Să presupunem că într-un anumit sistem de coordonate este începutul vectorului în punctul
iar la sfârșitul anului - la punctul