
Acasă | Despre noi | feedback-ul
7.1. invarianți statice. șurub dinamic
Anterior, sa constatat că vectorul principal al sistemului de forțe, poziționat arbitrar în spațiu,
(7.1) nu se schimbă cu o schimbare a centrului de conducere. Dar punctul principal nu este schimbat, iar noul centru actionarea determinată prin formula
. (7.2) unde - principalele puncte pentru aducerea centrelor de O și. Al doilea termen din partea dreaptă a formulei (7.2) reprezintă momentul vectorului rezultant aplicat pentru a aduce centrul O. relativ nou centru de conducere.
produsul scalar de ambele părți ale (7.2) de vectorul:
Deoarece vectorul perpendicular pe vectorul. atunci produsul lor scalar este zero. Prin urmare,
. (7.3), adică produsul scalar al vectorului principal al punctului principal nu depinde de aducerea centrului.
Astfel, atunci când schimbă centrul de conducere nu se schimba vectorul principal și produsul scalar al vectorului rezultant pe punctul principal. Ei spun că aceste valori sunt invariante în ceea ce privește alegerea de a aduce centrului.
Prima invariant statică numit vectorul principal. Într-un sens mai îngust al termenului de primul invariant înțeleagă piața principală a unității vector
Al doilea produs scalar invariant static se numește vectorul principal al punctului principal:
Din al doilea invariant urmează o consecință geometrică simplă. Într-adevăr, putem scrie ecuația (7.3), după cum urmează:
Fiecare dintre aceste produse este proiecția punctelor principale în direcția vectorului rezultant. În consecință, la schimbarea conducerii centrului de proiecție a punctelor principale în direcția vectorului rezultant nu este schimbat. Rețineți că, atunci când această investigație poate fi luată ca definiția celui de al doilea invariantului.
Deoarece proiecția punctelor principale în direcția vectorului rezultant nu se schimbă atunci când schimbă centrul de conducere, se poate afirma că pentru a aduce centru, în care vectorul rezultant și momentul dirijat de-a lungul aceleiași linii drepte, punctele principale ale modulului va fi minim. În acest caz, momentul rezultant este egal cu modulul de proiecție în direcția vectorului rezultant.
Este evident că proiecția punctelor principale în direcția vectorului rezultant este definit de
sau, ținând seama de valorile primul și al doilea invarianți
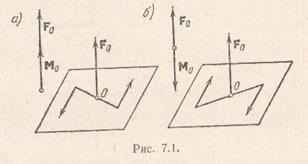
Un set de forțe și cuplu de forțe cu forța coliniare momentul, numit șurubul dinamic sau dinamită. Deoarece planul perpendicular pe punctul pereche pereche de acțiune, șurubul este un set dinamic de forță și perechea de forțe care acționează într-un plan perpendicular pe forță. Distinge șuruburi dinamice dreapta și stânga. Fig. arată șurub dreapta dinamică, formată din forță. sistem egal vector principal și cuplu forțe din cuplu. egală cu punctul principal; Fig. prezintă un șurub stânga, alcătuit din aceleași elemente.
Problema poate apărea, în care cazuri, acest sistem de alimentare poate duce la un joc Red Sox? Această întrebare se răspunde prin următoarea teoremă:
Dacă un al doilea invariant static nu este egal cu zero, sistemul de alimentare poate duce la un dinam. Această întrebare se răspunde prin următoarea teoremă:
Dacă a doua invarianta statică nu este egal cu zero, atunci sistemul poate duce la un dinam.
Să un punct arbitrar al sistemului se reduce la puterea egală cu vectorul principal. și o pereche de forțe cu momentul, egal cu punctul principal. Deoarece prin ipoteză. apoi ambele vector și. nu
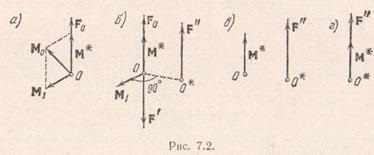
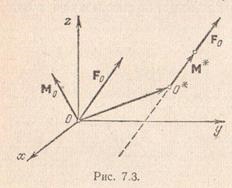
Ideea este nu numai în cazul în care sistemul de alimentare este redus la un dinam. De fapt, forța poate fi transferată de-a lungul liniei acțiunii sale, în momentul în care cuplul de forțe este liber vector, prin urmare, sistemul de forțe poate fi redus la Diname la toate punctele de linia dreaptă care trece prin punctul care linia de acțiune a forței. Această linie se numește axa centrală a sistemului de alimentare. Acum vom găsi axa centrală a ecuației.
Să - punctul axei centrale. Apoi, pentru acest punct al vectorului principal și punctul principal ar trebui să fie coliniare unele cu altele. Pe baza formulei (7.2) pentru punctul momentul rezultant poate fi scrisă ca
Condițiile colinearității a vectorului rezultant, iar timpul pentru punctul principal este scris după cum urmează:
în care - stabilirea șurub având o dimensiune de lungime.
Fie u - respectiv proiecția vectorului rezultant, iar principalele puncte pe axa x. y și z; atunci
Să coordonatele orice punct al axei centrale va fi de x. y. z. Prin urmare,
Substituind expresiile corespunzătoare din ecuația (7.7), obținem
Echivalând coeficienții versorii. și. avem