Băieți, să ne amintim de clasa a șaptea, iar graficul de „parabole“. După cum ne amintim, ecuația unei parabole: $ y = x ^ 2 = 1 * x ^ 2 $.
Și ce se întâmplă dacă înlocuim orice alt număr real în loc de unitate? Să ne uităm la două funcții: $ y = 2x ^ 2 $ și $ y = 0,5 * x ^ 2 $.
Am înființat un tabel de valori pentru fiecare dintre funcțiile. Să începem cu $ y = 2x ^ 2 $.
Pentru funcția $ y = 0,5 * x ^ 2 $. Luând act de punctul corespunzător de pe planul de coordonate și o linie care leagă-le, obținem următoarele grafice.
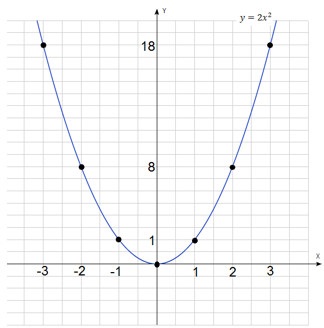
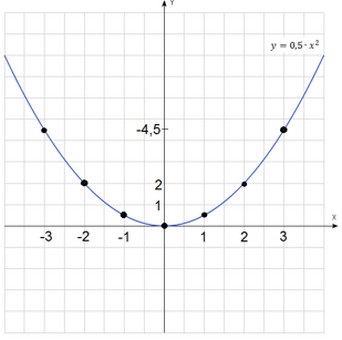
Ambele diagrame sunt similare între ele. Să-i atragă pe un plan de coordonate și să găsească asemănări și deosebiri.
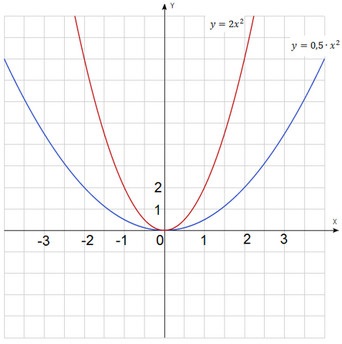
Fiecare dintre aceste grafice se numește parabole. Punctul cu coordonatele (0, 0) este numit vârful parabolei. Axa OY - axa de simetrie a parabolei. Ambele grafice sunt îndreptate în sus sau, cu alte cuvinte, spunând că „coarnele parabolei“ uita în sus. Graficele ale parabolei, putem descrie ecuația: $ y = kx ^ 2 $.
Dar aceste două grafice există diferențe. Una - mai lată decât cealaltă și caută mai lentă decât prima. Aceasta este o viteză parabole diferă. Cu cat mai mare coeficient de $ k $, cu atât mai repede parabolei caută în sus sau că acesta devine mai îngustă (pentru axa OY este apăsat). Este mai mic coeficient de $ k $, mai lent parabolei caută în sus sau mai mare devine (indepartandu-se de axa OY).
In cazul general, graficul parabolei $ y = ^ 2 $ KX, $ k> 0 $ este construit în același mod. Pentru început, se poate construi un tabel de valori și notează toate punctele după aderarea la ei o curbă. Dar toate vârful parabolei este la origine, ramurile sunt îndreptate în sus, iar axa ordonatelor este axa de simetrie a parabolei.
Și ce se va întâmpla în cazul în care coeficientul parabolei $ k $ 0 ° C. Filiala parabolei cu care se confruntă în jos, în cazul în care $ k $ 0 ° C. Pentru claritate, aici vom transfera una din graficele construite anterior.

Proprietăți ale funcției $ y = kx ^ 2 $, $ k> 0 $
1. Domeniul de determinare. Putem calcula valoarea funcției în orice punct de x. Apoi, funcția este definită ca hε $ (-∞ + ∞) $.
2. $ y = 0 $ la $ x = 0 $, $ y> 0 $ pentru $ x ≠ 0 $. Această proprietate este evident și în mod clar vizibile pe diagramă.
3. O funcție continuă. Program trece de linia solidă, punctele în care funcția nu este rupt.
4. Cea mai mare valoare nu este. Conform graficului arată că funcția este infinit merge în sus.
Cea mai mică valoare de $ y = 0, dacă $ $ $ x = 0. Pentru a găsi valoarea minimă ar trebui să fie pe grafic pentru a găsi cel mai jos punct. Acesta este punctul cu coordonatele $ (0; 0) $.
5. Funcția crește atunci când $ x> 0 $. Funcția scade pe măsură ce $ x $ 0.
6. Funcția este mărginită de mai sus printr-o $ y directă = 0 $.
7. Intervalul valorilor unei funcții: $ (- ∞; 0] $.
8. Funcția este convexă în sus.