Luați în considerare modul în care modificarea momentelor de inerție la rotirea axelor. Să ne momentele de inerție ale unei secțiuni transversale sunt în raport cu axa 0x. 0Y (nu neapărat centrală) -. - momentele de inerție axial. Pentru a fi determinată. - momente axiale în jurul axelor u. v. relativ răsucită în raport cu primul sistem la unghiul (Fig. 8)
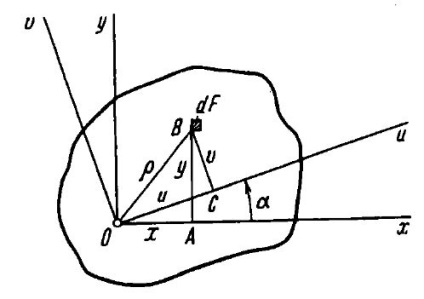
Având în vedere că proiecția OABC linie întreruptă egală cu proiecția de închidere, vom găsi:
Excludeți u și v în ceea ce privește momentele de inerție:
Luați în considerare primele două ecuații. Adăugarea lor pe termen de termen, obținem
Astfel, suma momentelor axiale de inerție în jurul a două axe perpendiculare între ele este independent de unghiul și rămâne constantă în timpul axelor de rotație. Menționăm aici că
În cazul în care - distanța de la origine la zona elementară (a se vedea figura 5.). astfel
În cazul în care - este deja familiar pentru noi în momentul de inerție polar:
Definim momentului de inerție axial în raport cu diametrul cercului.
Din moment ce, în virtutea simetrie, dar, după cum știți,
În consecință, pentru cercul
Odată cu schimbarea unghiului axei de rotație a cuplului și schimbare, dar suma rămâne neschimbat. În consecință, există o valoare. în care unul dintre momentele de inerție atinge valoarea sa maximă, în timp ce celălalt punct are o valoare minimă. Diferențierea unghiul și egalează derivatul la zero, vom găsi
La această valoare a unghiului unui al momentelor axiale va fi cel mai mare, iar celălalt - cel mai mic. Simultan, momentul de inerție centrifugal devine zero, este posibil să se verifice cu ușurință prin egalarea cu zero formula pentru momentul de inerție centrifugal.
Axele despre care momentul de inerție centrifugal egal cu zero, iar momentele axiale de a lua valori extreme numite axele principale. Dacă acestea sunt la același nivel central (punctul de origine coincide cu centrul de greutate al secțiunii transversale), atunci acestea sunt numite principalele axe centrale (u; v). Momentele de inerție axial aproximativ axele principale sunt numite momentele principale de inerție - și
Valoarea lor este determinată prin următoarea formulă:
Semnul plus corespunde momentului de inerție maxim, semnul minus - minim.
Există o geometrie mai caracteristici - gama inertsiisecheniya. Această valoare este adesea utilizată în constatările teoretice și calculele practice.
Raza de inerție față de o axă, de exemplu 0x, este o cantitate determinată din ecuația
F - aria secțiunii transversale,
- momentul de inerție axial,
Din definiția rezultă că raza de girație este distanța de la axa 0x, până la punctul în care să se concentreze (imaginar) aria secțiunii transversale F, un moment de inerție la acest punct a fost egal cu momentul de inerție al secțiunii transversale întreg. Cunoașterea momentului de inerție și o zonă, puteți găsi raza de inerție în jurul axei 0x:
Raza de girație corespunzătoare axelor principale, numite raze principale de girație și sunt determinate prin formulele