Titlul lucrării: Principalele axe și momentele principale ale inerție
Zona de subiect: Fizică
Descriere: Axa majoră și momentele principale de inerție axelor despre care momentul de inerție centrifugal este zero, numit axele principale (denumite uneori axe principale de inerție). Prin orice punct, luată în planul secțiunii, poate fi efectuată în cazul general.
Mărime fișier: 32,5 KB
Job descărcat: 65 de persoane.
Axele despre care momentul de inerție centrifugal este zero, numit axele principale (denumite uneori ca axe principale de inerție). Prin orice punct, luată în planul secțiunii, poate fi realizată, în general, o pereche de axe principale (în anumite cazuri speciale, poate exista un număr infinit). Pentru a verifica validitatea acestei declarații, să ne ia în considerare modul în care momentul de inerție centrifugal atunci când rotirea axei 90 „(fig. B7). Pentru un sit arbitrar dA, luată în primul cadran al axelor xy ale sistemului, ambele coordonate, și, prin urmare, produsul lor este pozitiv. În noul sistem de coordonate x, Ou „rotit în raport cu originalul 90, produsul a site-ului considerat coordonate este negativ. Valoarea absolută a acestui produs nu se schimbă, și anume. F. = Xv # 151; H1U. Evident. același lucru este valabil pentru orice alt domeniu elementar. Prin urmare, semnul sumei dAxy, momentul de inerție centrifugal la rotirea axei 90 „este inversată, adică. E. J = = # 151; J.
În procesul de rotație momentul de inerție centrifugal axe schimbări în mod continuu, prin urmare, cu o anumită poziție a axelor devine zero. Acestea sunt axa principală.
Deși am constatat că axa majoră poate fi trasă prin orice punct de intersecție, dar numai cei care trec prin centrul de greutate al secțiunii de interes practic # 151; axa centrală principală. Mai târziu, de regulă, de dragul concizie, vom le numim axele principale, omițând cuvântul „central“.
În cazul general al unei forme arbitrare a secțiunii transversale pentru determinarea poziției axelor principale este necesară efectuarea unei investigații speciale. Acolo ne limităm la secțiunile cazuri particulare având cel puțin o axă de simetrie (fig. 6.8).
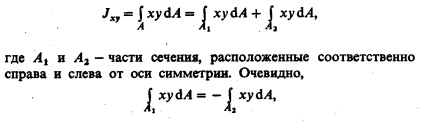
Prin. secțiune centrului de greutate axa Ox, Oy este perpendicular pe axa de simetrie, și definesc momentul centrifugal de inerție J. utiliza o proprietate cunoscută de matematica definit integral (suma este egală cu suma integralelor integral) și J s reprezintă suma a doi termeni:
pentru că, pentru orice zonă elementară la dreapta axei de simetrie, există o corespunzătoare din stânga, pentru care coordonează munca unui semn diferit.
Astfel, momentul de inerție centrifugal în jurul axelor Ox și Oy a fost egal cu zero, adică. E. Este axa majoră. Astfel, pentru a găsi secțiunea principală a axa de simetrie, este suficientă pentru a găsi poziția centrului său de greutate. Una dintre axa principală este axa centrală de simetrie, a doua axă perpendiculară pe acesta. Desigur, această dovadă rămâne valabilă în cazul în care axa perpendiculară pe axa de simetrie nu trece prin centrul de greutate al secțiunii transversale, adică. E. Axa de simetrie și orice perpendicular pe acesta, formează un sistem de axe principale.
Descentrată axa principală, așa cum sa menționat deja, nu prezintă interes.
Momentele de inerție axial față de axele centrale principale sunt numite momentele principale centrale (principal sau prescurtate) de inerție. Relativ la una dintre axele principale de inerție este maximă, în ceea ce privește celelalte # 151; minimă. De exemplu, secțiunea transversală prezentată în fig. 6.8 este momentul maxim de inerție J
(Comparativ cu axa Ox). Desigur, vorbind despre extremality momentele principale de inerție, ele înseamnă doar compararea lor cu alte momente de inerție, calculate în raport cu axa care trece prin același punct al secțiunii. Astfel, faptul că unul dintre momentele principale de inerție este maximă, iar celălalt # 151; minimă, poate fi considerată ca o explicație a ceea ce ei (n axele respective) sunt principalul. Egalitatea la zero a momentului de inerție centrifugal despre axele principale # 151; test de convenabil pentru a găsi Hx. Unele tipuri de secțiuni, de exemplu rotundă, hexagon pătrat, regulat și colab., (Fig. 6.9), au nenumărate principalele axe centrale. Pentru oricare dintre aceste secțiuni este axa centrală principală.
Fără a da probe, subliniem faptul că, în cazul în care două momente centrale principale de inerție egale una de alta, această secțiune axa centrală a principalelor oricare și toate momentele centrale majore de inerție sunt egale.
comunitățile științifice și tipurile lor istorice: școli academice colegiu invizibil. O altă formă comună de asociere informale de oameni de știință care joacă un rol semnificativ în dezvoltarea științei este școlile științifice. În ceea ce privește conținutul cel mai des pentru susținătorii școlii științifice se caracterizează printr-o abordare specifică a problemelor de cunoștințe și metode.