Axele principale de inerție și momentele principale de inerție.
Atunci când valorile unghiul Ix1, Iy1 și Ix1y1 schimbat. Am găsit unghiul la care Ix1 și Iy1imeyut valori extreme; acest lucru se va lua de la Ix1 Iy1 sau primul derivat de la zero și preravnyaem sale: iliotkuda (1.28)
Această formulă determină poziția celor două axe, în raport cu unul dintre care momentului de inerție axial este maximă, iar în raport cu celălalt - minemalen.
Acestea sunt numite axa principală. Momentele de inerție în jurul axelor principale sunt numite momentele principale de inerție.
Valorile momentelor principale de inerție se găsește din formulele (1.23) și (1,24), înlocuindu-le în formula (1.28), în timp ce folosind formule trigonometrice cunoscute pentru funcții unghiuri duble.
După transformare următoarea formulă pentru a determina momentele principale de inerție (1.29)
Explorarea derivata a doua poate fi stabilit că în acest caz (Ix
Axa principală care trece prin centrul de greutate al secțiunii, numit axele centrale principale.
În multe cazuri, este posibil să se determine imediat poziția axelor centrale principale. Dacă forma are o axă de simetrie, este una dintre principalele axe centrale, a doua trecere prin centrul de greutate al secțiunilor transversale perpendicular pe primul. Acest lucru rezultă din faptul că, în raport cu axa de simetrie și orice axă perpendiculară pe acesta, momentul de inerție centrifugal egal cu zero.
Dacă două momente centrale principale de inerție sunt egale, atunci oricare dintre secțiuni este axa principală, și toate momentele principale centrale de inerție sunt egale (un cerc, pătrat, hexagon, un hexagon echilateral).
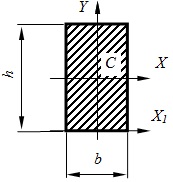
9.Osnovnye caracteristicile geometrice ale secțiunilor
Unde: C - centrul de greutate al secțiunilor plane;
A - aria secțiunii transversale;
Ix, Iy - momente axiale de inerție în jurul axelor principale;
IXI, iyi - momente de inerție axial față de axa auxiliară;
Ip - momentul de inerție polar;
Wp - momentul polar de rezistență
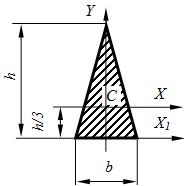
Secțiune transversală a unui triunghi isoscel
Tipuri de 10.Osnovnye de forțe care acționează asupra organismului. Momentul de forță în raport cu centrul. cuplu Proprietăți.
La Ras smot-re-SRI mi-ha-ni-che-ing sarcini durere-anvelope-TION forțe dei-stvu th-ing pe corp, nu poate-la-STi la cele trei axe-nou NYM diferite dar-un fel-dar-styam:
- puterea toată lumea, dar primul cha-de-cei-TION;
Toate organismele de-a-ing dna Bame au la-cha-Gi-va-TION-Xia pe Pământ, este OCU-cuvinte-les-dar dei Corolar, forțează toată lumea, dar primul cha-de-cho -niya. Dacă ne-am pre-nu-Bray-Causeway cu pro-TIV-le-no-l coș-do-ha, știm deja că toate corpurile pa-da-TION pe Pământ de la-la-la-vym ODI exprima check-in D-nor-l - exprimă check-in D-nor-it-sale de transfer, dar primul pas de-TION.
Precum și toate-tac înainte de a-, organismul, sub-ve-shen-ing pe PRU-zhine, Streit-mit-Xia se încadrează în jos din cauza cu-tine-bine-TION a Pământului, dar atunci când PRU Ms-on dis-cha-no-camping la Neko un corp de lungime roi rămâne-nav lee-va-et-HSIA, adică, atunci când ho-DIT în co-sută-me-me-ha-ni-che lea -sko egal-but-ve-Sia. Știm deja că mi-ha-ni-che-parametru egal-dar-ve-aceste lucruri pe-Stu-pas este atunci când suma DEI forțelor-stvu-lea ing pe corp este zero. Acest lucru se traduce cha este că puterea te-bine-IFPS, dei stvu-lea, care are ca scop o sarcină trebuie, pe ecuația-dar-ve-Sit-Xia, cu un fel de forță de roi dei stvu lea -schey cu sute-ro-HN PRU Ms HN. Această putere, la drepturile de in-evaluate pro-TIV forța te-bine și dei stvu STI-lea schaya cu sute-ro-HN forță PRU D-na HN, la-za-va-et-Xia de elasticitate lea stimul.
Proy AH-Neko o multime de lucruri dis-sute-I-set, un corp a fost lăsat-nav-lee-va-et-Xia, corp SKO-înălțime Micșorați Sha Xia este de la-provo-lea, dar cunoștințele Th-TION la zero, adică express check-D al organismului - ve-li-chi-na-cu-ri-ca Tel naya. Urmează-up-all-Tel-dar, pe corpul de o sută-ro-HN on-top-but-dei stvu-STI o forță într-un paradis-Streit-mit-Xia Ost-no-răsucire a corpului, adică dei stvu-un pro-TIV sale RMS-ro-STI. Această putere pe PS-VA-et-Xia vigoare TRE-TION.
Momentul de forță în jurul centrului (punct).
Momentul forței F în raport cu centrul (punctul) G este un mo vector (F) egal cu produsul vectorial al vectorul r raza. trase din centrul O la punctul A de aplicare a forței asupra vectorului forței F:
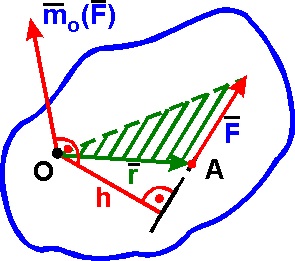
Vector mo (F) aplicată la punctul O și napravlenploskosti trecând prin centrul și siluF. în direcția din care forța tinde să transforme corpul vizibil în jurul centrului Oprotiv sensul acelor de ceasornic.
mo modul (F) este produsul modulului forță F pe umăr h:
unde h umărul scăzut perpendicular pe centrul O la forța F. Linia
mo de cuplu (F) caracterizează efectul forței F de rotație de la centru (punct) ON.
Proprietăți moment de forță:
1. Momentul forței despre centru nu se schimbă atunci când forța de transfer de-a lungul liniei acțiunii sale în orice punct;
2. Dacă linia forță de acțiune trece prin centrul (h = 0), momentul forței în jurul centrului Orav zero.