Probabilitatea dP ca o variabilă aleatoare continuă va lua valoarea aparținând intervalului (x. X + dx) este egal cu
,
unde f (x) - funcția de densitate de probabilitate (este probabilitatea ca pe unitatea de lungime a secțiunii în cauză).
Probabilitatea ca o variabilă aleatoare ia valori din intervalul [x1, x2] se calculează cu formula:
f (x) funcția prezintă următoarele informații importante: o valoare numerică x probabilitatea de a lua o valoare mai mare decât numărul de x1 și x2 este mai mică decât aria de sub curba f (x) în intervalul [x1. x2]. Desigur, acest lucru se aplică la orice x1 și x2. strâns legate sau la distanta oriunde pe linia x.
Printre cele mai cunoscute tipuri de distribuții de variabile aleatoare continue cele mai multe ori folosesc distribuția normală descrisă de legea lui Gauss. Pentru prima dată o lege normală a fost găsit în secolul H1H așa cum se aplică la eroarea de măsurare a teoriei Laplace și Gauss.

Gauss (Gauss) Karl Fridrih (30.04.1777, Braunschweig, - 02/23/1855, Goettingen), matematician german care a adus o contribuție fundamentală în astronomie și geodezie

Acum, după dovedit AM Lyapupovym teorema limitei centrale. A devenit clar de ce legea normală este larg răspândită în inginerie, biologie, sociologie, psihologie și multe alte domenii ale cunoașterii umane.

Lyapunov Aleksandr Mihaylovich [25.5 (6.6). 1857 Yaroslavl - 11.03.1918, Odesa], matematician român și inginer, academician al Academiei de Științe Petersburg.
Teorema limită centrală prevede că ori de câte ori o valoare aleatorie este generată prin adăugarea unui număr mare de variabile aleatoare independente cu variații finite, legea de distribuție a acestei variabile aleatoare este, practic, legea normală. Deoarece variabilele aleatoare sunt întotdeauna generează un număr infinit de motive, și, adesea, nici unul dintre ei are o variație, care este comparabil cu variația variabilei aleatoare, majoritatea care apar în practica de variabile aleatoare respectă o lege de distribuție normală.
De exemplu, înălțimea unui om, care este influențată de mai mulți factori, printre care masa nu este dominant în influența sa.
Distribuția normală, de asemenea, numit de distribuție Gauss sau de distribuție Gauss - o distribuție de probabilitate, care este specificată funcția de densitate de probabilitate:
în cazul în care parametrul # 956; - valoarea medie (așteptare) a unei variabile aleatoare și indică coordonatele maximul curbei de densitate de distribuție și # 963; ² - dispersie.
funcția de densitate de probabilitate a legii normale, și,
1.2 - grafice cu un mijloc # 956; și deviațiile standard diferite # 963;. și,
Graficul densității de probabilitate a legii de distribuție normală este simetrică cu linia verticală x max = # 956;. Și, la punctul de
x max = # 956; Funcția are un maxim egal.
În plus, aria de sub curba intreaga f (x) este 1, adică probabilitatea ca x pentru a ajunge la linia este egal cu 1, și este un eveniment semnificativ. Această proprietate este, de asemenea, numit condiția de normalizare.
schimbare # 956;. Puteți efectua deplasare paralelă a curbei f (x), de-a lungul axei x. De asemenea, se observă că cea mai probabilă apariția x în experiment apropiat # 956;. aria de sub f (x) la orice interval, care cuprinde # 956;. cel mai mare.
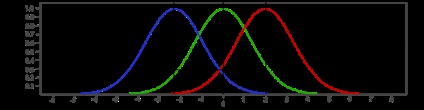
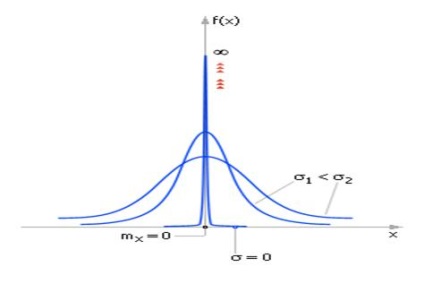
număr # 963; este abaterea medie a indicelui numeric al numărului x # 956;, mai puțin # 963;, de „cooler“ devine un „deal“ f (x), și mai puțin probabil să fie foarte diferită de x μ.
Dimpotrivă, la ridicat # 963; „Hill“ f (x) se extinde peste „câmpie“ și cu aproape egală probabilitate, poate apărea ca un apropiat # 956, și în mod arbitrar departe de # 956; .
Probabilitatea ca o variabilă aleatoare deviază de la așteptările sale matematice cu o valoare mai mare de trei ori abaterea standard este practic nulă.
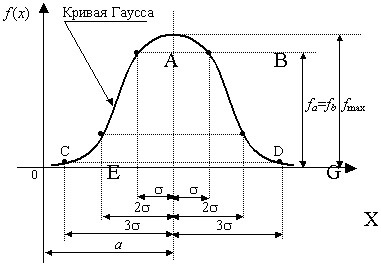
Calculele arată că probabilitatea unei variabile aleatoare distribuite în mod normal, în intervalul dintre următoarele:
I. P (μ- # 963; II. P (μ-2 # 963; III. P (μ-3 # 963; În practică, se crede că, dacă pentru unii - orice variabilă aleatoare este realizată de trei regula sigma, această variabilă aleatoare are o distribuție normală. distribuția Gauss - una dintre cele mai comune în fizică. O astfel de distribuție sunt supuse unor erori de măsurare a mărimilor fizice, rezultatele pentru tirul, distribuția proiecțiilor vitezelor moleculelor de gaz (distribuție Maxwell), probabilitatea de fluctuații mici, și mai mult.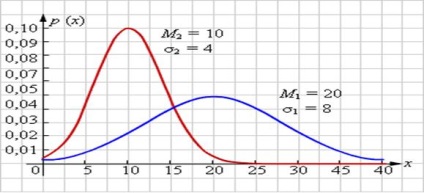
articole similare