Acesta vă permite să poziționați coeficienții binomiali pentru numere întregi non-negativ n. k în formă de triunghiul lui Pascal. în care fiecare număr este suma celor două părinte:
n = 0. n = 1. 1 1 1 n = 2 1 2 1 n = 3 1 3 3 1 n = 4. 1 4 6 4 1 ⋮ ⋮ ⋮ ⋮ ⋮ n = 0: 1 \\ n = 1 11 \\ n = 2: 121 \\ n = 3 1331 \\ n = 4: 14641 \\\ vdots \ vdots \ vdots \ vdots \ vdots \ Sfârșit >>
tabel triunghiulara propus de Pascal în lucrarea sa „Treatise pe triunghiul aritmetic“ (1654), diferă de aici, scrise de 45 ° rotit. Tabelele pentru coeficienții de imagine binomială au fost cunoscute anterior (Tartaglia. Khayyam O. și colab.).
Ațe în triunghiul lui Pascal, împărțit la 2 n> (suma tuturor numerelor într-un rând), în limita tinde la funcția de distribuție normală.
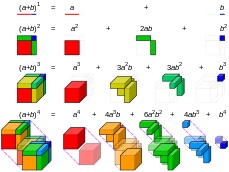
Vizualizare coeficienților binomiali până la nivelul 4
Vizualizare coeficienți binom până la nivelul 4 [1]
generatoare de funcții
Pentru valori fixe ale secvenței k funcția de generare de coeficienți binom (0 k). (1 k). (2 k). ...>, \;>, \;>, \; \ ldots> este:
Bidimensionala funcția de generare a coeficienților binomial (n k) >> pentru întreg n. k este:
- (N k) >> ⟺ este număr impar în notație binară nu reprezintă în rândurile unității k, unde numărul n zerouri.
- (N k) >> nekraten simplu p ⟺ în înregistrarea p ary număr k toate evacuările nu depășesc biții respectivi ai n.
- Secvența coeficienților binomial (n 0). (N 1). .... (N n)> \;> \; \ ldots, \; >>.
- toate numerele nu sunt multipli dat prim p ⟺ n = m p k - 1 -1>. în care numărul natural m
- toate numerele cu excepția prima și ultima sunt multipli de un anumit prim p ⟺ n = p k>;
- numărul de numere impare egal cu o putere a două (egală cu o putere de două numărul celor din reprezentarea binară a n);
- Acesta nu poate fi la fel de numere pare și impare;
- cdots nici multiple număr prim p număr egal (1 + 1) ⋯ (o m + 1) +1) \ (a_ + 1)>. în cazul în care numărul unui 1. .... o m \; \ ldots, \; a_> - p nivel -ary număr de înregistrare n; iar numărul m = ⌊ log p n ⌋ + 1 \ rfloor +1> - lungimea.
- toate numerele nu sunt multipli dat prim p ⟺ n = m p k - 1 -1>. în care numărul natural m
identitate de bază
Se obține prin calcularea coeficientului de x m + n> în identitate (1 + x) r (1 + x) s = (1 + x) r + s (1 + x) ^ = (1 + x) ^>. Suma este preluată de toate numere întregi k. pentru care termenul este diferit de zero. Pentru r reale arbitrare. s numărul de termeni nenuli în sumă este finită.
alte documente de identitate
raportul matrice
Dacă luăm matricea pătrată, conta N elemente cateta Pascal matrice triunghi și de cotitură pe oricare din cele patru colțuri, cele patru determinanți ai acestor matrice este egal cu ± 1 pentru orice N. mai mult decât atât determinant matrice cu vârful triunghiului în colțul din stânga sus este 1.
matrice din [(i + j i)]> \ end >> numere pe diagonală i + j = const rânduri de triunghiul lui Pascal repetate (i. J = 0,1, ...). Acesta poate fi descompus într-un produs de două matrici diagonale strict: triunghiular inferior și obținut de la ea de transpunere. Și anume:
Astfel, putem extinde matricea inversă la [(i + j i)]> \ end >> strict produsul a două matrici diagonale: prima matrice - o parte superioară, iar al doilea se obține din prima prin transpunere, care ne permite să dea o expresie explicită pentru elementele inverse:
elementele matricei inverse variază cu schimbarea dimensiunii sale și, spre deosebire de matricea de [(i + j i)]> \ end >>. nu este suficient pentru a atribui un nou rând și coloană. Coloana j a matricei din [(i + j i)]> \ end >> este un polinom de gradul j al argumentului i. De aceea, primele coloane p formează o bază completă pentru spațiul vectorilor de lungime p + 1, ale căror coordonate pot fi interpolate de un polinom mai mic sau egal -1 p. Rândul de jos al [(i + j i)] m. n - 1> \ end> _ ^> este ortogonal pe orice astfel de vector.
Atunci când un vector arbitrar de lungime p + 1 poate fi interpolate de un polinom de gradul I
\ End> _ ^> este zero. Folosind identitatea de mai sus și egalitatea scalare unităților matricei produsului rând inferior [(i + j i)] m. n - 1> \ end> _ ^> în ultima coloană a matricei [(i + j i)]> \ end >>. obținem:
Pentru înregistrare, puteți specifica o formulă p mai mare de recurență:
P 2 a + 2 (p) = Σ x = 1 p x P 2 a (x); un ⩾ 0; P 0 (p) = 1 _ (p) = \ sum _ ^x
_ (X) \ quad a \ geqslant 0; \ quad
_ (P) = 1>
Pentru a dovedi prima dovedesc identitatea:
Dacă doriți să găsiți o formulă pentru nu toate exponenți, atunci
Senior Q factor a - 1 (p) _ (p)> este 1, o-1 este necesară valori pentru a găsi alți factori:
Asymptotics și estimări
polinoame cu valori întregi
Este ușor de observat că coeficienții binomială (x 0) = 1. (x 1) = x. (X2) = x 2 2 - x 2. ...> = 1,> = x,> = >> -> \ puncte> sunt polinoame evaluate număr întreg al lui x. și anume ia valori întregi pentru valori întregi ale lui x. Mai mult, ele formează o bază polinoame cu valori întregi, în care toate polinoamele sunt exprimate sub formă de combinații liniare cu coeficienți întregi cu valori întregi. [1]
În același timp, standardul de bază 1. Baza x. x 2. ..., \ dots> nu este posibil să se exprime toate polinoamele întregi, folosind doar coeficienți întregi, așa cum este (x 2) = x 2 2 - x 2> = >> - >> are o coeficienți fractionare de puteri ale lui x.
Acest rezultat poate fi generalizat la polinoame în mai multe variabile. Și anume, în cazul polinomul R (x 1 .... X m), \ puncte, x _)> gradul k are coeficienți reali și ia valori întregi pentru valori întregi de variabile,
unde P - este un polinom cu coeficienți întregi. [2]
Coeficienții binom poate fi calculată cu ajutorul formulei (n k) = (n - 1, k) + (n - 1 k - 1)> => + >>. în cazul în care, la fiecare pas pentru a stoca valori (n k) >>, atunci când k = 0. 1. .... n. Acest algoritm este deosebit de eficient, dacă doriți să obțineți toate valorile (n k) >> a n fixă. Algoritmul necesită O (n) de stocare (O (n 2))> efectuate pe unitatea de timp în calcularea tuturor tabelelor Coeficienți binom) și O (n 2))> timp (presupunând că fiecare număr ocupă de o memorie și operații cu numere) .
Pentru o valoare fixă de k coeficienți binom poate fi calculat prin formula recurență (n k) = n n - k ⋅ (n - 1, k)> => \ cdot >> cu valoarea inițială (k) = 1> = 1>. Pentru a calcula valoarea (n k) >> această metodă necesită O (1) memorie și O dată (n).
Dacă este necesar să se calculeze coeficienții (nk) >> o valoare fixă de n poate folosi formula (nk) = nk + 1, k ⋅ (nk - 1)> => \ cdot >> cu setarea inițială (n 0) = 1> = 1>. La fiecare iterație pas scade numărătorul 1 (valoarea n inițială), respectiv, iar numitorul este mărit cu 1 (valoarea inițială 1). Pentru a calcula valoarea (n k) >> această metodă necesită O (1) memorie și O (k) timp.