Această aplicație foarte importantă ne vom concentra asupra coeficienților binomiali, sau, mai degrabă, extinderea acestora la valori arbitrare ale SuperScript. Uneori, o temă în literatura de specialitate se numește „extins triunghiul lui Pascal“, deoarece extinderea coeficienților binomiali presupune o extensie a triunghiului lui Pascal, care dintre acești factori este, precum și luate în considerare aici funcția (1 + z) n (mai precis, extinderea sa în serie) se numește binom în apropiere.
Proprietățile coeficienților binomiali și dovedesc identități de bază în această secțiune nu este furnizat, vorbim despre ele numai în contextul funcțiilor generatoare. Se presupune că cititorul este familiarizat cu prevederile de bază ale combinatorica, sau cel puțin le-a întâlnit în viața reală. La urma urmei, matematica ne înconjoară din toate părțile. Numere, modele și diverse combinații pot apărea oriunde: în timpul călătoriei la magazin, calculând șansele de a câștiga la cazino, în teoria de control și chiar previziuni futuriste. În general, toți știu cum să numere. Dar, uneori, combinatorică este mult mai complexă decât este necesar în viața de zi cu zi. De exemplu, în calculul entropia unui sistem fizic complex, atunci când este necesar pentru a calcula numărul de configurații valide model fizic corespunzătoare. Coeficienții Deci avansați binomiali doar mai relevante pentru calcule științifice, nu de zi cu zi.
definiții de bază
Aici am un pic de oprire pe definițiile și notație, pentru a evita orice neînțelegeri. Pregătit de cititorul poate sări peste acest pas.
Coeficientul de binom notat. sau (care este adesea găsit în literatura rusă).
Să definim doar niște simboluri. Desemnarea corectă pentru coeficienții binomiali nu sunt. atât predate în școlile din România (și universități), precum și. Din păcate, nu știu motivul pentru care România este mai utilizat în mod obișnuit denumire. și în restul lumii -. Prin urmare, vă rugăm să rețineți că, dacă scrie un articol pentru o revistă românească, veți înțelege modul în care nu sunt identificate în mod corespunzător acești factori și vă sfătuim să scrie pentru reviste străine.
Citiți caracterul în multe feluri, „numărul de combinații de n pentru k», sau pur și simplu „de n k», precum și spunând că „alegerea lui k n». Semnificația acestor expresii este închisă într-o interpretare combinatorie a acestui personaj - un număr de moduri de a alege obiecte k de obiecte n distincte, iar ordinea nu este importantă. De exemplu, pot fi alese două elemente ale unei multitudini de zece moduri:
În general, se știe că
În procesul de calcul, să nu fie considerate factoriale de prisos, putem reduce imediat o parte din factorii:
Din această formulă și va construi în viitor. Aceasta este definiția corectă a coeficienților binomiali. Numărul n se numește indicele k și superioară - inferioară. În conformitate cu interpretarea combinatorie a n și k trebuie să fie întreg non-negativ. Provocarea noastra va fi de a extinde definiția la valoarea arbitrară a lui n.
coeficienți binom, ordonate într-un mod special pentru a forma un triunghi de Pascal.
În secolul al XVII-lea francez matematician, fizician și filosof Blez Paskal pentru prima dată în „Treatise pe triunghiul aritmetic“ sa descris mai detaliat cu privire la proprietățile triunghiului în sine (deși triunghiul găsit în lucrările altor matematicieni cu mult înainte de Pascal).
Construit acest triunghi mare este foarte simplu:
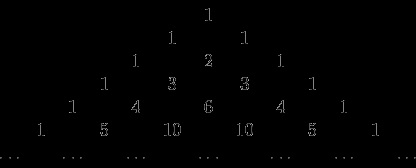
De-a lungul marginilor unităților de triunghi sunt plasate, și orice număr de picioare nu pe margine, se calculează ca suma a două numere este situat în partea din dreapta sus in stanga si. De exemplu, 10 = 4 + 6. sau 1 + 3 = 2. Deci, vorbim despre triunghiul lui Pascal se datorează faptului că el a format doar coeficienții binomiali:
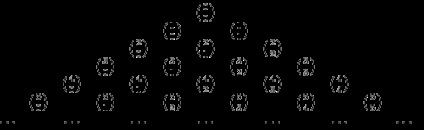
Pentru scopurile noastre (și pentru comoditate) este mai bine pentru a înregistra triunghiul, aliniindu-l la marginea din stânga:

Zeros apar datorită zero în numărătorul (când k> n). Rețineți că unitățile sunt plasate în coloana de zero, ca
Numărătorul este produsul dintre numărul zero elemente este prin definiție egal cu 1. Formula este corectă pentru toți (inclusiv complex) n.
Ei bine, ne apropiem de faptul că pentru a studia coeficienții binomiali pentru toți n. extensia noastră în primul rând, trebuie să fie de așa natură încât formula a rămas aceeași (pentru comoditate), și în al doilea rând, Pascal triunghi format de coeficienții binomiali (cu o valoare a indicelui negativ), nu trebuie să-și piardă proprietățile de bază:
citește că numărul din celula (n, k) este suma din stânga sus și de sus (atunci când numărul de aliniat spre stânga).
In al treilea rand (cel mai important), trebuie să rămână loială teorema binomială, a cărui declarație se amintește în paragraful următor.
teorema binom
Această expresie este numită teorema binomială. coeficienții binomială și Newton se numesc coeficienții binomiali.
Acum, folosind teorema binomială și triunghiul lui Pascal, poate fi calculat, de exemplu, (al treilea triunghi care are loc)
Acest site este dedicat funcțiilor generatoare, așa că avem această teoremă este interesată numai în această poziție. Scriem funcția de generare, după cum urmează:
Prezentată funcția de generare de secvență generează coeficienții binomiali cu un egal superscript la n. Exponent în suma poate fi scris egal cu ∞. nu se schimbă nimic, atunci când n este un non-negativ (de ce?). Rețineți că z = substituție 1 oferă o identitate remarcabilă (număr de finală, astfel încât substituția este validă):
care arată că suma tuturor numerelor din n-lea rând de triunghiul lui Pascal este egal cu doi, ridicat la puterea n.
Această extindere a funcției (1 + z) n într-un număr consistent cu formula Taylor, în conformitate cu care coeficienții zk este egală cu
Permiteți-mi să vă reamintesc că această funcție este o serie Taylor converge pentru | z |<1 (когда n произвольно). Эта функция также носит название «Биномиальный ряд».
extensie
Acum suntem interesați de răspunsul la întrebarea dacă puteți preveni în teorema binomială că n este un întreg negativ? Tu poți, cu triunghiul lui Pascal extinde „în sus“, singura cale, dacă vrem să mențină proprietățile sale de bază:
în același timp. Luați în considerare linia negativă mai mult:

De exemplu, minus prima linie a triunghiului poate fi la fel ca asta, și nici o altă cale, pentru că. în timp ce elementele rămase sunt calculate în mod explicit:
Care sunt avansate coeficienții binomiali? Pentru a stabili o serie de fracții simple. De exemplu,
Acum obținem o formulă pentru întregul coeficienților binomiali negative pe baza nu pe poziția lor în triunghiul, ci din definiția lor corectă:
Această formulă este, de asemenea, în conformitate cu extinderea acestei funcții în seria Taylor pentru | z |<1.
Hai. În practică, pot fi exponenți raționale utile, de exemplu, să considerăm seria binomială la n = 1/2.
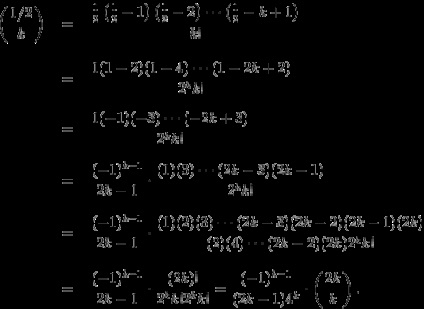
Această formulă ne oferă o oportunitate de a stabili o serie de funcții
In mod similar (părăsim o derivare detaliată a cititorului)
și acest lucru, la rândul său, vă permite să înregistrați o mai funcție de generare utilă:
Este vorba despre un număr de binom și locul său în teoria funcțiilor generatoare. Cazuri speciale ale indicelui binom: n - un număr întreg, și n = ± 1/2.