O scurtă descriere a documentului:
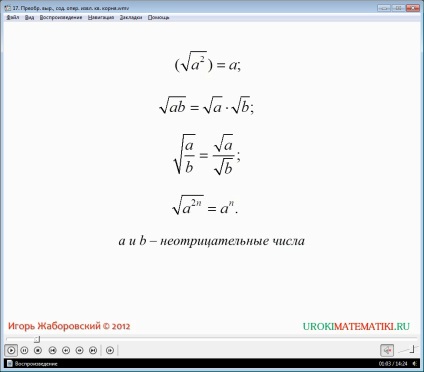
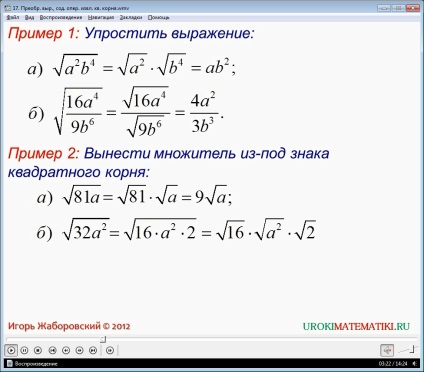
Exemplele în care expresia de conversie necesară care conține rădăcina pătrată. Este indicat faptul că, în aceste exemple, cu condiția ca Au b sunt numere non-negative. În primul exemplu trebuie simplificate √16a exprimare 4 / 9b și 4 √a 2 b 4. În primul caz, se aplică proprietăți care indică faptul că rădăcina pătrată a produsului a două numere este egală cu produsul dintre rădăcinile acestora. Ca rezultat al expresiei de conversie se obține ab 2. În a doua expresie este folosită formula transformării rădăcinii pătrate a privat în rădăcini private. Rezultatul transformării este 4a expresie 2 / 3b 3.
În al doilea exemplu trebuie să fie scos de sub semnul pătrat rădăcină multiplicator. Soluția expresiilor √81a, √32a 2. √9a 7 b 5. De exemplu, patru expresii de conversie sunt prezentate ca aplicate transformare rădăcină formula produsului de mai multe numere pentru rezolvarea acestor probleme. Individul există cazuri când expresiile conțin coeficienți numerici, parametrii din chiar, gradul de ciudat. Ca urmare, expresia de conversie obținut √81a = 9√a, √32a 2 = 4a√2, √9a 7 b 5 b 3 = 3a 2 √ab.
În al treilea exemplu, este necesar să se efectueze o operațiune opusă celei în problema anterioară. Factorul de sol sub semnul rădăcină pătrată trebuie să fie, de asemenea, posibilitatea de a utiliza formulele studiate. Acesta a oferit în termeni 2√2 și 3a√b / √3a face multiplicatorul înainte de paranteze sub semnul rădăcinii. Folosind binecunoscuta formulă, factorul stând în fața semnului rădăcină, pătrat și plasat sub forma unui factor în lucrarea sub semnul rădăcină. In prima expresie este obținută prin transformarea expresiei √8. Formula produsului cal este aplicat mai întâi în a doua expresie pentru a converti numărătorul și apoi formula rădăcinii privat - pentru a transforma întreaga expresie. După reducerea numărătorul și numitorul în radicand, se pare √3ab.
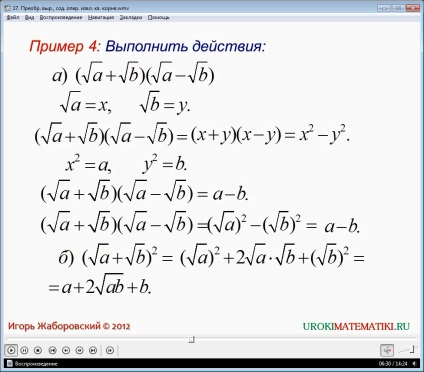
În exemplul 4, trebuie să urmați pașii din expresiile (√a + √b) (√a-√b). Pentru a rezolva această expresie introduce noi variabile, înlocuind monoamele conținând semnul rădăcinii √a = x și y = √b. după substituirea noi variabile este evident capacitatea de a folosi formule de multiplicare prescurtate, atunci expresia devine forma x 2 Y2- Revenind la variabilele originale, obținem un-b. A doua expresie (√a + √b) 2 pot fi transformați prin înmulțirea Acronimul Formula. După extinderea obține rezultatul unui + 2√ab + b.
În exemplul 5, descompunerea se realizează pe expresiile multiplicatorilor 4a-4√ab + b + 1 și h√h. trebuie să efectuați conversia, să identifice factorii comuni pentru rezolvarea acestei probleme. Dupa aplicarea pătrat proprietăți rădăcină la soluții de prima diferență sumă expresie este convertită într-un pătrat (2√a-√b) 2. Pentru soluțiile de a doua expresie trebuie să fie înregistrată în factorul rădăcină la un semn de rădăcină, apoi aplicați formula sumei cuburi. Rezultând din conversie devine expresie (√h + 1) (x 2 -√h + 1).
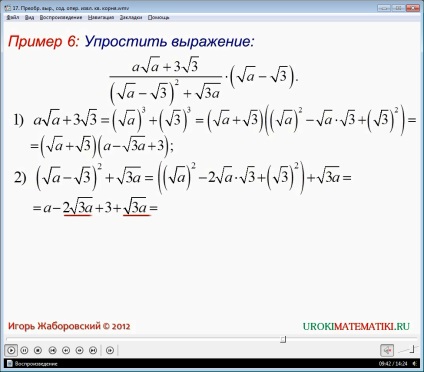
Exemplul 6 prezintă o soluție în care este necesară simplificarea ecuației (a√a + 3√3) (√a-√3) / ((√a-√3) 2 + √3a). decizie de stabilire se realizează în patru etape. În prima etapă numărătorul este transformat într-un produs cu multiplicare Acronim formulă - Cuburi suma a două numere. In al doilea act este transformat numitorul, care devine un fel de-√3a + 3. După conversia devine posibilă reducerea fracției. În ultimul act, de asemenea, se aplică o formulă de multiplicare prescurtate, care ajută pentru a obține rezultatul final și 3.
În al șaptelea exemplu, pentru a scăpa de rădăcina pătrată în numitorul fracțiunilor 1 / √2, 1 / (√3-√2). La rezolvarea sarcinilor folosind proprietatea fracțiuni de bază. Pentru a scapa de rădăcină la numitor, numărătorul și numitorul sunt multiplicate cu același număr, cu care este pătrat de expresie radicală. Ca rezultat al calculelor obținem 1 / √2 = √2 / 2 și 1 / (√3-√2) = √3 + √2.