Reprezentarea numerelor în calculator
Datele numerice sunt prelucrate într-un calculator în notație binară. Numerele sunt stocate în memorie în cod binar, adică. E. O secvență de zerouri și cele, și pot fi prezentate sub forma unui număr fix sau virgulă mobilă.
Numerele întregi sunt stocate în memorie în formatul punct fix. Într-un astfel de format pentru stocarea reprezentărilor numerelor întregi nenegative asignate registru de memorie care conține opt celule de memorie (8 biți). Fiecare categorie corespunde celulei de memorie este întotdeauna același număr de descărcare de gestiune, și imediat după virgulă este LSB și de descărcare este grila. De exemplu, numărul 11001101 este stocat în memoria registru, după cum urmează:
Valoarea maximă a unui număr întreg nenegativ, care poate fi stocat într-un registru în formatul unui punct fix poate fi determinată din formula: 2 - 1, unde n - numărul de cifre ale numărului. Numărul maxim în acest caz este egal cu 2 - 1 = 255 = 0 min 11111111i = 00000000. Astfel, intervalul de numere întregi non-negative vor fi în intervalul de la 0 la 255.
În contrast cu sistemul zecimal în sistemul numeric binar într-o reprezentare calculator a numărului binar sunt simboluri care reprezintă semnul numărului: pozitiv (+) sau negativ (-), astfel încât să reprezinte numere întregi semnate în sistem binar utilizează două formate pentru numere: formatul valorii semnat și un format cod suplimentar. În primul caz, pentru stocarea numerelor întregi semnate alocate două registre de memorie (16 biți), MSB (stânga) este utilizat sub semnul numărului dacă numărul este pozitiv, bitul de semn 0 este scris dacă numărul este negativ, atunci - 1. exemplu Numărul 536 = 0000001000011000budet reprezentat în memorie registre, după cum urmează:
un număr negativ -536 = 1000001000011000 sub forma:
Numărul maxim de valoare minimă pozitivă sau negativă a numărului format (reprezentări pe baza de descărcare sub marca) este 2 - 1 = 2 - 1 = 2 - 1 = 32767 = 111111111111111 și gama de numere va fi în intervalul -32767-32767.
Cel mai adesea pentru a reprezenta numere întregi semnate în sistem binar format de cod se aplică suplimentar care vă permite să înlocuiți o operație de scădere aritmetică în operațiunile informatice de plus, care simplifică foarte mult structura microprocesorului și crește viteza.
Pentru a reprezenta numere întregi negative, într-un format utilizat de un cod suplimentar, care reprezintă unitatea adăugarea unui număr negativ la zero. Traducerea numărului negativ întreg în codul adițional se realizează prin următoarele operațiuni:
1) Modul de scriere directă a codului în n (n = 16) biți;
2) pentru a primi codul de retur al numărului (numărul pentru a inversa toate biți, adică toate unitățile înlocuite cu zerouri, și zerouri - în unitate) ..;
3) codul invers rezultat pentru a adăuga unul la LSB.
De exemplu, pentru numărul de -536 în acest modul format va fi egal cod 0000001000011000 invers - 1111110111100111, și codul suplimentar - 1111110111101000. verifica valoarea de cod suplimentare obținute cu ajutorul calculatorului. Pentru a face acest lucru, introduceți o valoare de -536 modul, adică. E. Numărul 536, și folosind butonul opțional Bin, conversia acestui număr reprezentat în notația zecimală, în sistemul binar după instalarea butonului opțional de 2 octeți. Nu apăsați butonul calculator pentru a obține înapoi numărul de cod, și adăugarea la unitatea de cod binar opus, - codul suplimentar. Rezultatul final a fost obținut în fereastra Câmp Calculator (Fig. 2.6). Puteți face chiar mai ușor: tastarea pe un calculator numărul -536i de activare buton Bin. obține mai mult codul pentru acest număr în sistemul binar.
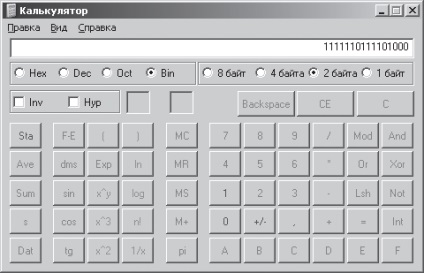
Fig. 2.6. Rezultat generează cod suplimentar
Trebuie amintit faptul că codul suplimentar un număr pozitiv - numărul în sine.
Pentru a stoca numere întregi semnate, în plus față de performanță de calcul pe 16 biți, atunci când două registre de memorie (acest format număr este numit, de asemenea, formatul scurt de numere întregi cu semn), formate din mediu și lung numere întregi semnate aplicate. Pentru reprezentarea numerelor în formatul mediilor utilizate patru registre (4 x 8 = 32 biți), iar pentru reprezentarea numerelor în formatul numerelor întregi lungi - opt registre (8 x 8 = 64 biți). Intervalele de valori pentru mărimea numerelor medii și lungi sunt respectiv egale cu: - (2 - 1) ... + 2 - 1 si - (2-1) ... + 2 - 1.
Reprezentarea numerelor de calculator în format punct fix are avantajele și dezavantajele sale. Avantajele includ ușurința de reprezentare a numerelor și algoritmi pentru punerea în aplicare a operațiilor aritmetice, deficiențele - reprezentarea finală a gamei de numere care nu poate fi suficient pentru a rezolva multe probleme practice (matematică, economică, fizică, etc ...).
numere reale (zecimale finite și infinite) sunt prelucrate și stocate într-un calculator în format virgulă mobilă. Cu acest format de prezentare a punctului zecimal în înregistrare poate varia. Orice număr real Rk format în virgulă mobilă poate fi reprezentat ca:
unde A - număr de mantisă; h - radix; p - numărul de ordine.
Expresia (2.7) pentru sistemul număr zecimal ia forma:
Această formă de reprezentare a numărului este, de asemenea, numit normal. Odată cu schimbarea în ordinea virgulei în numărul de ture, adică. E. În ceea ce plutește spre stânga sau spre dreapta. Prin urmare, reprezentarea sub formă normală a numerelor se numește forma de virgulă mobilă. Decimal 15.5, de exemplu, un format de virgulă flotantă poate fi reprezentată ca: 0,155 · 10; 1,55 · 10; 15,5 · 10; 155,0 · 10; 1550.0 · T și 10. D. Această notație 15,5 zecimale în virgulă mobilă nu este utilizat pentru a scrie programe de calculator, și le introduceți la calculator (dispozitive de intrare calculator percep numai de înregistrare a datelor liniar). Pe baza acestei expresie (2.7) pentru numerele zecimale și le introduceți într-un computer pentru a transforma mintea
unde F - numărul de ordine,
.. Adică în loc de radix 10 a scrie sistemul litera E, în locul punctului zecimal - punctul, și multiplicarea semnului nu este atribuit. Astfel, numărul 15.5 în format plutitoare punct și de înregistrare liniară (reprezentare calculator) vor fi scrise sub forma: 0.155E2; 1.55E1; 15.5E0; 155.0E-1; 1550.0E-2, etc.
Indiferent de sistemul de numere sub formă de orice număr de virgulă flotantă poate fi reprezentată printr-un set infinit de numere. Această formă de scriere se numește non-normalizată. Pentru o reprezentare lipsită de ambiguitate a plutitoare numere de puncte, folosind un număr normalizat sub formă de înregistrare la care numărul de mantisă trebuie să îndeplinească condiția
în cazul în care | A | - valoarea absolută a mantisei.
Condiția (2.9) înseamnă că mantisa trebuie să fie corect și să aibă o șansă după numărul zecimal, care este diferit de zero, sau, cu alte cuvinte, în cazul în care după virgulă în mantisa ar trebui să nu este zero, atunci numărul se numește normalizat. Astfel, numărul 15.5 în formă normalizată (mantisa normalizată) sub formă de virgulă flotantă va fi după cum urmează: .. 0,155 · 10, adică mantisei normalizate va fi A = 0,155 și ordinea P = 2, sau în reprezentarea pe calculator a numărului 0.155E2 .
Numerele sub formă de virgulă mobilă au un format fix și în memoria calculatorului ocupă patru (32 de biți) sau opt octeți (64 de biți). În cazul în care numărul de ia în memorie pe 32 de biți a computerului, acesta este numărul de o singură precizie, în cazul în care 64 de biți, acest număr dublu-precizie. Când se înregistrează numărul de biți plutitoare punctiforme sunt alocate pentru stocarea semnului mantisa, semnul ordinului, iar ordinea mantisei. Numărul de biți, care este dat de numărul de ordine, definește intervalul de schimbare a numerelor, precum și numărul de biți alocate pentru a stoca mantisei - precizia cu care numărul dat.
Atunci când se efectuează operații aritmetice (adunare și scădere) pe numerele reprezentate în format virgulă mobilă, a implementat următoarea procedură (algoritm):
1) sunt aliniate numerele de ordine pe care se efectuează operații aritmetice (procedura număr modulo mai mic este crescută la o valoare de ordin superior modulo numărul, mantisa este scăzut în aceeași perioadă de timp);
2) efectuează operații aritmetice cu numere mantise;
3) normalizarea rezultatului este realizată.
Să ilustrăm cele de mai sus cu exemple.
Efectuăm adăugarea a două numere de 0,5 și 0,8 · 10 · 10 în formatul virgulă mobilă.
Egal ordine de aliniere mantiselor și adăugarea de 0,05 x 10 + 0,8 x 10 = 0,85 * 10 0,85 Mantisa rezultată este normalizat, ca condiție satisface (2.9).
Efectuăm adăugarea a două numere de 0,1 și 0,1 · 2 · 2 în format virgulă mobilă.
Egal ordine de aliniere și adăugarea de mantise: 0.01 · 2 + 2 = 0,1 · 0,11 · 0,11 2. mantisa rezultată este normalizat ca condiție satisface (2.9).