Numere complexe. număr complex este numărul de forma z = a + biabRi2 = -1
Notă.
Numărul real al unui - este partea reală a lui z și este notat un = Rez
Numărul real de b - este partea imaginară a lui z și este notat b = Imz
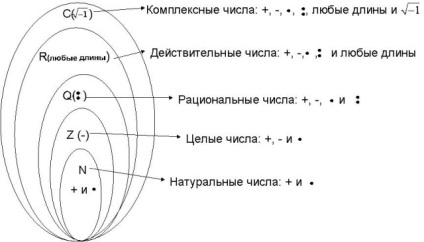
Numerele reale sunt un set complet de numere și operații pe ele, care pare a fi suficient pentru a rezolva toate sarcinile de matematica. Dar cum să rezolve această ecuație în numere reale x2 + 1 = 0? Mai există un număr de extensie - numere complexe. Numerele complexe pot fi luate din rădăcinile de numere negative.
forma algebrică a unui număr complex. formă algebrică a unui număr complex are vidz = a + bi (aRbRi2 = -1)
Notă. Dacă un număr = rez = 0b = Imz = 0, atunci z este numit imaginar. Dacă a = rez = 0b = Imz = 0, atunci numărul numit z pur imaginar
Interpretarea geometrică a numerelor reale este o linie reală. În plus, pe linia reală „nu există nici un loc pentru noi puncte“, adică orice punct de pe axa reală corespunde unui număr real. Prin urmare, numerele complexe de pe această linie nu poate fi poziționat, dar puteți încerca să ia în considerare, împreună cu axa reală pe care o vom amâna partea reală a unui număr complex, o axă mai perpendicular pe acesta; noi o numim axa imaginară. Apoi, orice z = a + ib număr complex poate fi pus în corespondență cu punctul de coordonate carteziene. Pe axa orizontală am complot partea reală a numărului complex, iar axa verticală - o parte imaginar. Aceasta stabilește un one-o corespondență între toate numerele complexe și toate punctele în plan. În cazul în care este construit această linie, planul de coordonate numit planul complex. Interpretarea numărului complex z = a + b i este un OA vector cu coordonate (a, b), pornind de la punctul O (0,0) și se termină la punctul A (a, b)
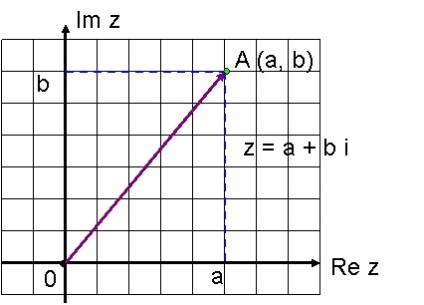
Conjugate. Numărul z = a + bi, și z = o-bi sunt numere complexe conjugate
Proprietatea. Suma și produsul a două numere complexe conjugate sunt numere reale: z + z = 2azz = a2 + b2
invers aditiv. și numere complexe opuse -Z = -a-bi Numărul z = a + bi numit.
Proprietatea. Suma a două numere complexe opuse este zero:
z + (- z) = 0
Numere egale. Două numere complexe se spune că sunt egale dacă acestea sunt părțile reale și imaginare.
Acțiuni cu numere complexe, date în formă algebrică:
proprietatea adăugării: Suma a două numere complexe z1 = a + bi și z2 = c + di este numărul complex de forma z = z1 + z2 = a + bi + c + di = a + c + (b + d) i
Exemplu: 5 + 3i + 3i = 8 + 2i
Proprietate scăderea: Diferența dintre două numere complexe z1 = a + bi și z2 = c + di este numărul complex de forma z = z1-z2 = a + bi-c + di = a-c + (b-d) i
Proprietate înmulțind: Produsul a două numere complexe z1 = a + bi și z2 = c + di este numărul complex de forma z = z1z2 = a + bic + di = ac-bd + (ad + bc) i
împărțirea Property Auto două numere complexe z1 = a + bi și z2 = c + di este numărul complex vidaz = z2z1 = c + dia + = bi + c2 + d2ac bd + c2 + d2bc-adi
Acțiuni cu numere complexe date în formă trigonometric
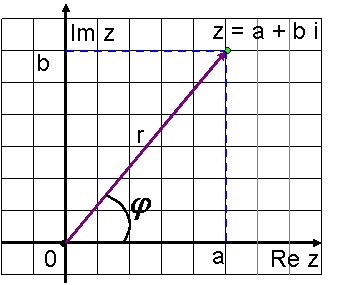
Înregistrarea unui complex număr z = a + bi în formă z = rcos + numit ISIN formă trigonometrică a unui număr complex.
Număr complex Modul: r = a2 + b2
Argumentul unui număr complex: cos = Rasin = rb

Numere complexe și imaginari
Luați în considerare ecuația pătratică incompletă:
x 2 = a,
în cazul în care o - o cantitate cunoscută. Soluția acestei ecuații poate fi scrisă ca:
Există trei posibilități:
1). A = 0. Dacă x = 0 atunci.
în cazul în care a, b - numere reale, i - unitate imaginară.
EXEMPLU EXEMPLU numere complexe s 3 + 4 i. 7-13.6 i. 0 + 25 25 i = i. 2 + i.
Familiarizarea cu numerele imaginare și complexe, se referă la „numere imaginare și complexe.“ Necesitatea unui nou tip de numere au apărut în rezolvarea ecuațiilor de gradul doi în cazul D
Înmulțind numărătorul și numitorul său de 2 + 3i
și completarea toate schimbările, obținem:
Reprezentarea geometrică a numerelor complexe. Numerele reale sunt reprezentate prin puncte pe linia numerică: unde A reprezintă numărul punctului 3, punctul B - numărul 2 și O - zero. În schimb, numerele complexe sunt reprezentate de puncte pe planul de coordonate. Am ales această formă dreptunghiulară (cartezian) coordonează cu aceeași scală de pe ambele axe. Apoi, un număr complex + bibudet reprezentat prin punctul P cu abscisa și ordonata a b (a se vedea. Fig.). Acest sistem de coordonate se numește planul complex.
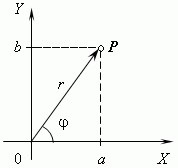
Modulul numărului complex este lungimea PO vector, reprezentând un număr complex pe planul de coordonate (complex). număr complex + un modul bi este desemnat | a + bi | sau o literă și r este egal cu:
Numerele complexe Conjugat au același modul. __
Argumentul unui număr complex - este unghiul dintre axa OX și PO vector, reprezentând un număr complex. Prin urmare, tan = b / a.
forma trigonometrică a unui număr complex. Abscisa a și ordonata b a unui număr complex a + bi poate fi exprimată prin modulul r, și un argument.
Operații cu numere complexe reprezentate printr-un formular trigonometrice.
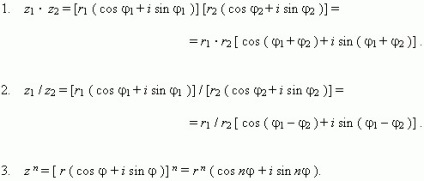
Această formulă celebru Moivre.
Aici k - unitate. Pentru a obține diferite valori ale rădăcinii n n-lea putere a lui z este necesară pentru a specifica valori pentru n k consecutive (de exemplu, k = 0, 1, 2, ..., n - 1).