Reprezentarea distribuției fluxului de energie consumată de motor cu inducție de la rețea, furnizează schema energetică prezentată în Fig. 7, care prezintă structura completă a pierderii de putere care rezultă din motor asincron trifazat se execută.
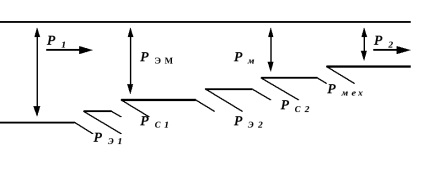
P1 = 3U1I1 cos1 putere -active furnizată motorului de la rețea; m1 - numărul fazelor înfășurării statorului; U1, tensiune de fază I1 și curentului statoric fazei PE1 = 3R1I12 - pierderea de energie electrică în înfășurarea rezistenței (pierderea de cupru) active stator;
PM1 = Ps1 = Pg + Pb - Pierderi de putere în circuitul magnetic stator, egal cu suma pierderilor de putere pe histerezisul și (pierderea stator de fier) curenți turbionari;
Ps2 = PM2 - pierderile de putere în circuitul magnetic al rotorului, egal cu suma pierderilor de putere asupra histerezisului și curenții turbionari în rotor;
PE2 = - pierderile de energie electrică în înfășurări (pierdere de cupru) ale rotorului;
Pmeh - pierdere de putere mecanică în motor (pierderile generate de frecare în lagăre și prin rezistența aerului la rotirea rotorului);
Pm - puterea dezvoltată de motor, cu pierderea de putere mecanică în acesta;
P2 = 2 = Mn2 / 9,55 - puterea efectivă a arborelui rotorului motorului; 2 = 2n2 / 60 = 2 / p - viteza rotorului unghiular.
Pentru scopuri practice, putem neglija pierderile mecanice datorate frecării mici și a pierderilor magnetice ale rotorului, deoarece rotorul frecvența curentă a mai multor hertzi. Cu o astfel de frecvență de curent și deci câmpul magnetic al pierderilor de rotor sunt mici. Prin urmare, putem presupune că PEM = Pm + PE2 = 1; Pm = P2 = 2; ceea ce implică faptul că pierderea de putere este proporțională cu cuplul rotorului și alunecare:
rotitoare electromagnetică și momentele critice ale unui motor cu inducție, caracteristicile sale mecanice
Cuplul motorului asincron poate fi determinată din formula motorului P2 = puterea mecanică 2. echivalând-l la valoarea de rezistorovR'2 electric de putere (1-s) / s pentru toate cele trei faze pe circuitul echivalent din Fig. 6.
I'2 reprodus curent rotor poate fi exprimată în termeni de parametrii circuitului echivalent al motorului de inducție (vezi. Fig. 6), având în vedere faptul că impedanța circuitului de magnetizare mult mai complet stator rezistență bobinaj, r. F.
Dat fiind ca rezultat al rotorului de expresie I2 curent pentru a obține caracteristica timp-alunecare:
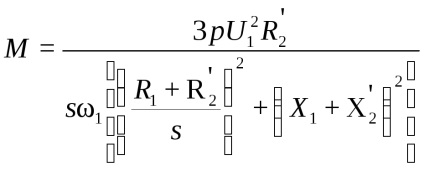
Formula arată că timpul a motorului de inducție proporțională cu pătratul tensiunii aplicate, și depinde de alunecare. Mai mult decât atât, există un motor cu rotor culisant în care se dezvoltă cel mai mare (critic) momentMk. Rotorul maxim skolzheniesk (critic) care corespunde timpului critic al motorului de inducție, poate fi găsit prin luarea derivatul chitanței timp (neglijarea activă statoraR1 rezistență datorită înfășurării sale relativ mici) și egalează-l la zero. Când etomsk = R'2 / (X1 + X'2).
Substituind rotor culisant sc în formula instant (luând în considerare chtoR1 = 0), obținem o expresie pentru momentul critic al motorului de inducție:
Înlocuind în expresia pentru parametrii de timp sc IMC. Obținem o expresie pentru momentul motorului de inducție, înregistrate prin momentul critic și alunecare:
.
Dependența timpului de inducție cu motor de alunecare a rotorului M (s), construită conform ecuației obținută are forma prezentată în Fig. 8, de asemenea. Această relație este de fapt o caracteristică mecanică a motorului de inducție (compară cu curba prezentată în figura 8b.), Deoarece viteza rotorului este legat de alunecarea acestuia sootnosheniemn2 = n1 (1-s).
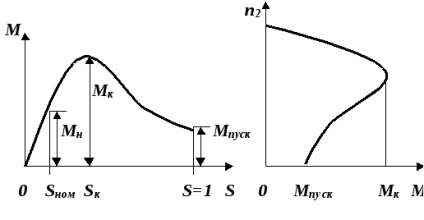
Analiza arată că, în intervalul de diapozitive de la s = 0 dos = sc caracteristică mecanică este stabilă, deci kakdM / ds> 0; cu creșterea sarcinii pe arborele are loc creșterea cuplului dezvoltat de motor. În același timp, în intervalul de diapozitive sc = = OTS 1 dos caracteristică mecanică a motorului de inducție devine instabil deoarece kakdM / ds<0.
Deoarece alunecare între rotor și turația motorului de inducție există o relație directă, apoi prin specificarea culisantă viteza rotorului, poate fi reprezentată dependența motor de inducție a vitezei de rotație de timp n2 curba (M), prezentat în Fig. 8b. care se numește caracteristica mecanică a motorului de inducție.