Ce concluzie se poate trage din faptul că mediana unui triunghi este înălțimea.
Dacă mediana unui triunghi este înălțimea, acest triunghi - isoscel.
CF - înălțime și mediană
Δ ABC - isoscel.
În primul rând vom sublinia dovada. Ceea ce înseamnă că triunghiul este isoscel? Acest lucru înseamnă că el are două laturi sunt egale. Deci, avem nevoie pentru a dovedi că Δ ABC două părți sunt egale: AC = BC. Egalitatea părților rezultă din egalitatea de triunghiuri. Prin urmare, vom avea nevoie pentru a dovedi că cele două triunghiuri. Ce? Δ AFC și Δ BFC.
Ce știm de declarația lor problemă? CF - înălțime, atunci CF este perpendicular AB, astfel încât unghiurile AFC și BFC - linii.
Chiar și noi știm că CF - mediană. Deci, ea împarte partea AB în două părți egale: AF = BF. Astfel, două din cele trei puncte pentru a dovedi că triunghiuri au deja.
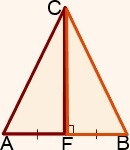
Această tehnică ne permite să vedem că partea CF - totală.
Trei puncte acolo.
Vom proceda la înregistrarea probelor.
Luați în considerare Δ AFC și Δ BFC.
1) ∠AFC = ∠BFC = 90º (din CF - înălțimea triunghiului stării ABC).
2) AF = BF (din CF - triunghi median ABC cu condiția).
3) Side CF - totală.
Prin urmare, Δ AFC = Δ BFC (două laturi și unghiul dintre ele).
Din egalitatea triunghiurilor presupune egalitatea părților în cauză: AC = BC. Prin urmare, Δ ABC - isoscel AB cu bază (așa cum este definit de triunghiul isoscel).
QED.
În cazul în care înălțimea triunghiului și toate medianele coincid, atunci triunghiul - echilateral (la fiecare două părți sunt egale între ele, prin urmare, toate cele trei laturi sunt egale).