Benzile de interferență de grosime egală într-un film subțire, adică benzi întunecate sau luminoase corespunzătoare valorii constante a grosimii filmului (d), se poate observa în întrefierul dintre contactării unul cu celălalt de o suprafață placă plană și suprafața sferică convexă a lentilei (vezi. Figura 5).
În acest caz, grosimea stratului de aer crește treptat de la centrul lentilei până la marginile sale. În cazul incidenței normale (perpendiculare la suprafață), benzile de grosime egală au forma cercurilor concentrice, numite inele Newton.
Dacă un fascicul de lumină monocromatică cade pe lentilă, atunci undele luminoase reflectate de la limitele superioare și inferioare ale stratului de aer interferează unul cu celălalt.
Deoarece, în contrast cu exemplul dat mai sus, reflexia undei luminii are loc la punctul B pe mediul de aer din sticlă, și nu sticla aer în Fig.4, se adaugă X / 2 la sumand L1 și formula (19) în partea inițială va arăta:
Aceasta este diferența de cale optică, în acest caz este egală cu dublul grosimii spațiului de aer (2d) (indicele de refracție al aerului = 1).
În cele din urmă, obținem:
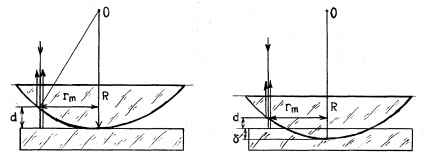
Figura 5. Schema de apariție Fig.6. Deformarea contabilă
Inelele lui Newton
Se formează inele întunecate, unde diferența de cale optică este egală cu un număr impar de jumătăți de undă (a se vedea 16):
și anume la o grosime de lovitură
unde m = 0,1,2,3. numărul de inel.
Raza inelului negru m (rm) este determinată din triunghiul AOC (vezi figura 5)
unde R este raza de curbură a cristalinului. Presupunând că valoarea spațiului de aer la locul inelelor este mic (adică d "R), putem scrie:
Din această formulă se poate observa că raza de curbură a lentilei poate fi găsită prin măsurarea razei inelului Newton și a cantității de spațiu de aer la locul de origine al inelului. Raza inelelor lui Newton poate fi măsurată folosind un microscop care are o scală de măsurare. Pentru a nu măsura dimensiunea decalajului (apropo, nu este clar cum se procedează experimental), se poate folosi condiția de interferență pentru apariția inelelor întunecate (24).
Apoi, raza de curbură a lentilei poate fi exprimată în funcție de raza inelului lui Newton, lungimea de undă a luminii utilizate și numărul de inel care trebuie măsurat:
Folosind formula (28) pentru a determina raza de curbură poate duce la o eroare, deoarece un punct de lentile de contact și deformarea plăcii de sticlă de lentile este posibilă în mărime comparabilă cu lungimea de undă a luminii, astfel încât utilizarea de terminale bazate pe Figura 5 (a se vedea. formula 26,27,28) va fi incorectă.
Valoarea experimentală observată a spațiului de aer poate fi mai mică decât valoarea teoretică obținută din figura 5 prin deformarea plăcii de sticlă și a lentilei (δ) (vezi figura 6). Prin urmare, într-un experiment real în formula (27) în loc de grosimea fantei de aer (d) cantitatea necesară pentru a substitui grosimea fantei de aer și mărimea deformării lentilei și placă de sticlă (d + δ) .Given că starea de apariție a unui inel închis (24) este determinată numai de grosimea diferenței, obținem următoarea formulă care conectează razele inelelor lui Newton cu raza de curbură a cristalinului:
Este mai convenabil experimental înlocuirea razei inelului Newton cu diametrul său (Dm). În acest caz, formula (29) va avea forma:
De la (30), se vede că pătratul diametrului inelelor Newton (dm2) este proporțională cu numărul ordinal al inelului (m) .Dacă reprezentate grafic dm2 = f (m), punctele experimentale trebuie să se întindă pe o linie dreaptă, iar panta acestei linii drepte (α ) va fi egal mod .tak 4Rλ pentru a găsi raza de curbură a lentilei este necesar, folosind graficul dm2 = f (m), pentru a găsi
și apoi calculați raza de curbură a cristalinului prin formula:
Datorită deformării, în centrul lentilei se observă un punct negru circular care corespunde grosimii zero a spațiului de aer. Măsurarea diametrului punctului închis central (inelul lui Newton, al cărui număr este m = 0), poate determina valoarea deformării lentilei prin formula: